第83页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
1.(2024·甘孜州中考)如图,正六边形ABCDEF内接于⊙O,OA= 1,则AB的长为(

A.2
B.$\sqrt{3}$
C.1
D.$\frac{1}{2}$
C
).
A.2
B.$\sqrt{3}$
C.1
D.$\frac{1}{2}$
答案:
C [解析]
∵正六边形ABCDEF内接于⊙O,
∴∠AOB=$\frac{1}{6}$×360°=60°.
∵OA=OB,
∴△AOB是等边三角形,
∴AB=OA=1.故选C;
∵正六边形ABCDEF内接于⊙O,
∴∠AOB=$\frac{1}{6}$×360°=60°.
∵OA=OB,
∴△AOB是等边三角形,
∴AB=OA=1.故选C;
2.(2024·德阳中考)已知,正六边形ABCDEF的面积为$6\sqrt{3}$,则正六边形的边长为( ).
A.1
B.$\sqrt{3}$
C.2
D.4
A.1
B.$\sqrt{3}$
C.2
D.4
答案:
C [解析]如图,连接OA、OB,过点O作OM⊥AB,垂足为M.
∵六边形ABCDEF是正六边形,
∴∠AOB=360°÷6=60°.
∵OA=OB,
∴△AOB是正三角形,
∴OA=OB=AB.设AB=x,则OA=OB=x,AM=$\frac{1}{2}$OA=$\frac{x}{2}$,
∴OM=$\frac{\sqrt{3}x}{2}$
∴S正六边形=6S△AOB=6$\sqrt{3}$,
∴6×$\frac{1}{2}$×x×$\frac{\sqrt{3}}{2}$x=6$\sqrt{3}$,解得x=2或x=−2<0(舍去),即正六边形的边长为2.故选C.
C [解析]如图,连接OA、OB,过点O作OM⊥AB,垂足为M.
∵六边形ABCDEF是正六边形,
∴∠AOB=360°÷6=60°.
∵OA=OB,
∴△AOB是正三角形,
∴OA=OB=AB.设AB=x,则OA=OB=x,AM=$\frac{1}{2}$OA=$\frac{x}{2}$,
∴OM=$\frac{\sqrt{3}x}{2}$
∴S正六边形=6S△AOB=6$\sqrt{3}$,
∴6×$\frac{1}{2}$×x×$\frac{\sqrt{3}}{2}$x=6$\sqrt{3}$,解得x=2或x=−2<0(舍去),即正六边形的边长为2.故选C.

3.(2024·青岛中考)为筹备运动会,小松制作了如图所示的宣传牌,在正五边形ABCDE和正方形CDFG中,CF、DG的延长线分别交AE、AB于点M、N,则∠FME的度数是(

A.90°
B.99°
C.108°
D.135°
B
).
A.90°
B.99°
C.108°
D.135°
答案:
B [解析]
∵五边形ABCDE是正五边形,
∴∠CDE=∠E=$\frac{(5−2)×180°}{5}$=108°.
∵四边形CDFG为正方形,
∴∠CDF=90°,∠CFD=45°,
∴∠FDE=108°−90°=18°,∠DFM=180°−45°=135°,
∴∠FME=360°−18°−135°−108°=99°.故选B.
∵五边形ABCDE是正五边形,
∴∠CDE=∠E=$\frac{(5−2)×180°}{5}$=108°.
∵四边形CDFG为正方形,
∴∠CDF=90°,∠CFD=45°,
∴∠FDE=108°−90°=18°,∠DFM=180°−45°=135°,
∴∠FME=360°−18°−135°−108°=99°.故选B.
4.(2024·镇江中考)如图,AB是⊙O的内接正n边形的一边,点C在⊙O上,∠ACB= 18°,则n= ______.


10
答案:
10 [解析]
∵∠ACB=18°,
∴∠AOB=2∠ACB=2×18°=36°,
∴n=360°÷36°=10.
∵∠ACB=18°,
∴∠AOB=2∠ACB=2×18°=36°,
∴n=360°÷36°=10.
5. 如图,正方形ABCD内接于⊙O,其边长为2,则⊙O的内接正三角形EFG的边长为______.
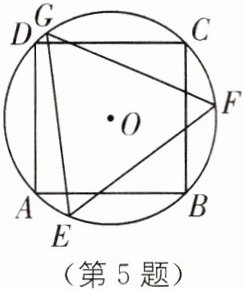

答案:
$\sqrt{6}$ [解析]如图,连接AC、OE、OF,过点O作OM⊥EF于点M.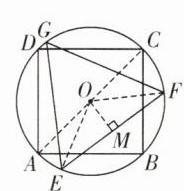
∵四边形ABCD是正方形,
∴AB=BC=2,∠ABC=90°,
∴AC是直径,AC=2$\sqrt{2}$
∴OE=OF=$\sqrt{2}$.
∵OM⊥EF,
∴EM=MF.
∵△EFG是等边三角形,
∴∠GEF=60°,在Rt△OME中,
∵OE=$\sqrt{2}$,∠OEM=$\frac{1}{2}$∠GEF=30°,
∴OM=$\frac{\sqrt{2}}{2}$,EM=$\sqrt{3}$OM=$\frac{\sqrt{6}}{2}$
∴EF=$\sqrt{6}$.
$\sqrt{6}$ [解析]如图,连接AC、OE、OF,过点O作OM⊥EF于点M.

∵四边形ABCD是正方形,
∴AB=BC=2,∠ABC=90°,
∴AC是直径,AC=2$\sqrt{2}$
∴OE=OF=$\sqrt{2}$.
∵OM⊥EF,
∴EM=MF.
∵△EFG是等边三角形,
∴∠GEF=60°,在Rt△OME中,
∵OE=$\sqrt{2}$,∠OEM=$\frac{1}{2}$∠GEF=30°,
∴OM=$\frac{\sqrt{2}}{2}$,EM=$\sqrt{3}$OM=$\frac{\sqrt{6}}{2}$
∴EF=$\sqrt{6}$.
6. 传统文化 司南 (2025·扬州广陵区期中)司南是我国古代辨别方向用的一种仪器.其早在战国时期就已被发明,是现在所用指南针的始祖.如图(2),司南中心为一圆形,圆心为点O,直径为20,根据八个方位将圆形八等分(图(2)中点A~H),过点E作⊙O的切线与AG的延长线交于点M,连接EG.
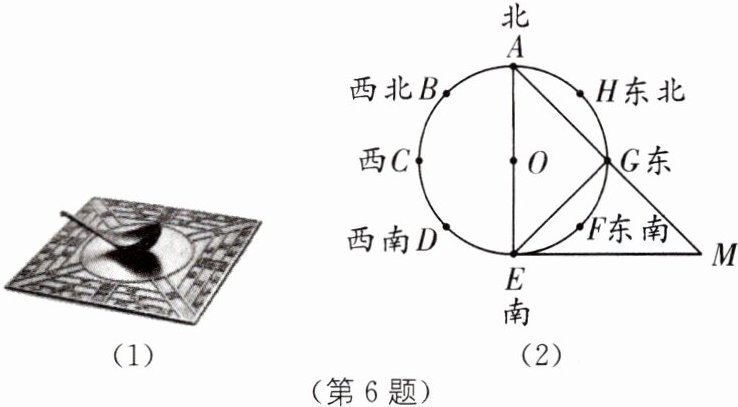
(1)相邻两个方位间所夹的圆心角的度数为
(2)求AG的长;
(3)求ME的长.

(1)相邻两个方位间所夹的圆心角的度数为
45°
;(2)求AG的长;
∵AE为⊙O的直径,∴∠AGE=90°.∵$\stackrel{\frown}{AG}$=$\stackrel{\frown}{EG}$,∴AG=EG,∴∠GAE=∠AEG=45°,∴AG=EG=10$\sqrt{2}$
(3)求ME的长.
∵ME为⊙O的切线,∴∠AEM=90°,由(2)知∠GAE=45°,∴ME=AE=20.
答案:
(1)45°
(2)
∵AE为⊙O的直径,
∴∠AGE=90°.
∵$\stackrel{\frown}{AG}$=$\stackrel{\frown}{EG}$,
∴AG=EG,
∴∠GAE=∠AEG=45°,
∴AG=EG=10$\sqrt{2}$
(3)
∵ME为⊙O的切线,
∴∠AEM=90°,由
(2)知∠GAE=45°,
∴ME=AE=20.
(1)45°
(2)
∵AE为⊙O的直径,
∴∠AGE=90°.
∵$\stackrel{\frown}{AG}$=$\stackrel{\frown}{EG}$,
∴AG=EG,
∴∠GAE=∠AEG=45°,
∴AG=EG=10$\sqrt{2}$
(3)
∵ME为⊙O的切线,
∴∠AEM=90°,由
(2)知∠GAE=45°,
∴ME=AE=20.
7.(2024·泰州泰兴期末)我们知道,五边形具有不稳定性,正五边形OABCD在平面直角坐标系中的位置如图(1)所示,点A在x轴负半轴上,固定边AO,将正五边形向右推,使点A、B、C共线,且点C落在y轴上,如图(2)所示,此时∠CDO的度数为(
A.108°
B.120°
C.135°
D.150°
B
).A.108°
B.120°
C.135°
D.150°
答案:
B [解析]
∵五边形OABCD是正五边形,
∴OA=AB=BC=CD=DO,
∴在Rt△AOC中,OA=$\frac{1}{2}$AC,
∴∠OCA=30°.连接OB,则OB=$\frac{1}{2}$AC=BC=CD=OD,
∴四边形OBCD是菱形,
∴∠OCD=∠OCB=30°,
∴∠ODC=180°−30°×2=120°.故选B.
∵五边形OABCD是正五边形,
∴OA=AB=BC=CD=DO,
∴在Rt△AOC中,OA=$\frac{1}{2}$AC,
∴∠OCA=30°.连接OB,则OB=$\frac{1}{2}$AC=BC=CD=OD,
∴四边形OBCD是菱形,
∴∠OCD=∠OCB=30°,
∴∠ODC=180°−30°×2=120°.故选B.
查看更多完整答案,请扫码查看


