《2025年实验班提优训练九年级数学上册苏科版》

8. 传统文化 古钱币 如图,一枚圆形古钱币的中间是一个正方形孔,已知圆的直径与正方形的对角线之比为3:1,则圆的面积约为正方形面积的( ).

A.27倍
B.14倍
C.9倍
D.3倍

答案：
B　[解析]如图,设AB=6a,因为CD:AB=1:3,所以CD=2a,OA=3a.因此正方形的面积为$\frac{1}{2}$CD·CD=2a²,圆的面积为π×(3a)²=9πa²,所以圆的面积是正方形面积的9πa²÷(2a²)≈14(倍).故选B.

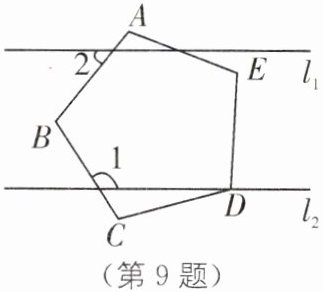
9. 如图,五边形ABCDE是正五边形.若$l_{1}// l_{2}$,则∠1-∠2= ______°.

答案：
72　[解析]如图,过点B作BF//l₁，与DE交于点F,由正五边形的性质，得∠ABC=108°,
∵l₁//BF//l₂,
∴∠2=∠ABF,∠1+∠CBF=180°,
∴∠2+180°−∠1=108°,即∠1−∠2=72°.解后反思　本题考查了多边形的内角、平行线的性质，关键是熟练掌握正五边形的性质.

10.(2024·苏州中考)铁艺花窗是园林设计中常见的装饰元素.如图是一个花瓣造型的花窗示意图,由六条等弧连接而成,六条弧所对应的弦构成一个正六边形,中心为点O,$\overset{\frown}{AB}$所在圆的圆心C恰好是△ABO的内心,若$AB= 2\sqrt{3}$,则花窗的周长(图中实线部分的长度)= ______.(结果保留π)

答案：
8π　[解析]如图,过点C作CM⊥AB 于点M,则AM=BM=$\frac{1}{2}$AB=$\sqrt{3}$.
∵六条等弧所对应的弦构成一个正六边形,中心为点O,
∴∠AOB=360°÷6=60°,
∴△AOB是正三角形,
∵点O是△AOB的内心，
∴∠CAB=∠CBA=$\frac{1}{2}$×60°=30°,∠ACB=2∠AOB=120°,在Rt△ACM中,AM=$\sqrt{3}$,∠CAM=30°,
∴AC=2CM,由勾股定理易得AC=2,
∴$\stackrel{\frown}{AB}$的长为$\frac{120π×2}{180}$=$\frac{4}{3}$π,
∴花窗的周长为$\frac{4}{3}$π×6=8π.

11. 如图,正六边形ABCDEF的边长为2,点P在对角线AC上,∠EDP= 75°,PQ⊥EF于点Q,则PQ的长是______.

答案：
2$\sqrt{3}$−1　[解析]如图,过点E作EJ⊥AC于点J,过点D 作DK⊥EJ于点K,过点Q作QM⊥EJ于点M,过点P 作PN⊥QM于点N,则四边形PNMJ是矩形，四边形DKJC是矩形,设PQ=m.
∵∠DEF=∠EDC=120°,∠EDP=75°,
∴∠PDC=45°,
∵∠DCP=90°,
∴∠CDP=∠CPD=45°,
∴CP=CD=2.
∵PQ⊥EF,
∴∠PQE=90°,
∴∠DPQ=360°−75°−120°−90°=75°.易得∠DPN=45°,
∴∠QPN=30°,
∴NQ=$\frac{1}{2}$m,MJ=PN=$\frac{\sqrt{3}}{2}$m.在Rt△DEK中,∠EDK=30°,DE=2,
∴EK=1,
∴EM+PN=EK+KJ=3.
∵CJ=DK=$\sqrt{3}$,
∴MN=PJ=2-$\sqrt{3}$
∴QM=$\frac{1}{2}$m+2-$\sqrt{3}$
∵∠EQM=30°,
∴EQ=2EM,由勾股定理，得EM=$\frac{\sqrt{3}}{3}$QM=$\frac{\sqrt{3}}{3}$($\frac{1}{2}$m+2-$\sqrt{3}$),
∴3=$\frac{\sqrt{3}}{3}$($\frac{1}{2}$m+2-$\sqrt{3}$)+$\frac{\sqrt{3}}{2}$m,
∴m=2$\sqrt{3}$−1,
∴PQ=2$\sqrt{3}$−1.

12. 手拉手模型 如图,正方形ABCD内接于⊙O,点E是$\overset{\frown}{BC}$的中点,连接AE、DE、CE.
(1)求证:AE= DE；
(2)若CE= 1,求四边形AECD的面积.

答案：

(1)
∵四边形ABCD是正方形,
∴AB=CD,
∴$\stackrel{\frown}{AB}$=$\stackrel{\frown}{CD}$.
∵点E是$\stackrel{\frown}{BC}$的中点，
∴$\stackrel{\frown}{BE}$=$\stackrel{\frown}{EC}$
∴$\stackrel{\frown}{AB}$+$\stackrel{\frown}{BE}$=$\stackrel{\frown}{CD}$+$\stackrel{\frown}{EC}$，即$\stackrel{\frown}{AE}$=$\stackrel{\frown}{DE}$，
∴AE=DE.
(2)如图,连接BD、AO过点D作DF⊥DE交EC的延长线于F.利用手拉手模型证全等
∵四边形ABCD是正方形，
∴∠DBC=∠DEC=45°,DA=DC.
∵∠EDF=90°,
∴∠F=∠90°−∠DEF=45°,
∴DE=DF.
∵∠AED=$\frac{1}{2}$∠AOD=45°,
∴∠AED=∠F=45°.
∵∠ADC=∠EDF=90°,
∴∠ADE+∠EDC=∠CDF+∠EDC=90°,
∴∠ADE=∠CDF.在△ADE和△CDF中，$\left\{ \begin{array}{l} ∠AED=∠F, \\ ∠ADE=∠CDF, \\ DA=DC, \end{array} \right.$
∴△ADE≌△CDF(AAS),
∴AE=CF,S_△ADE=S_△CDF,
∴S_{四边形AECD}=S_△DEF.
∵EF=$\sqrt{2}$DE=EC+CF=EC+DE,EC=1,
∴1+DE=$\sqrt{2}$DE,
∴DE=$\sqrt{2}$+1,
∴S_{四边形AECD}=S_△DEF=$\frac{1}{2}$DE²=$\sqrt{2}$+$\frac{3}{2}$.解后反思　本题考查正多边形与圆、正方形的性质、全等三角形的判定和性质、等腰直角三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形,属于中考常考题型.

13. 如图,⊙O半径为4 cm,正六边形ABCDEF为其内接正六边形,点P、Q同时分别从A、D两点出发,以1 cm/s的速度沿AF、DC向终点F、C运动,连接PB、QE、PE、BQ.设运动时间为t s.
(1)求证:四边形PEQB为平行四边形；
(2)填空：
①当t=2时,四边形PBQE为菱形；
②当t=0或4时,四边形PBQE为矩形.

答案：
(1)
∵正六边形ABCDEF内接于⊙O,
∴AB=BC=CD=DE=EF=FA,∠A=∠ABC=∠C=∠D=∠DEF=∠F.
∵点P、Q同时分别从A、D两点出发,以1cm/s的速度沿AF、DC向终点F、C运动,
∴AP=DQ=tcm,PF=QC=(4−t)cm.在△ABP和△DEQ中$\left\{ \begin{array}{l} AB=DE, \\ ∠A=∠D, \\ AP=DQ, \end{array} \right.$
∴△ABP≌△DEQ(SAS),
∴BP=EQ.同理可证PE=QB,
∴四边形PEQB为平行四边形.
(2)①2　[解析]当PA=PF,QC=QD时,四边形PBQE 为菱形,此时t=2.②0或4　[解析]当t=0时,∠EPF=∠PEF=30°,
∴∠BPE=120°−30°=90°,
∴此时四边形PBQE为矩形.当t=4时,同理可知∠BPE=90°,此时四边形PBQE为矩形.综上，当t=0或4时，四边形PBQE为矩形.