《2025年实验班提优训练九年级数学上册苏科版》

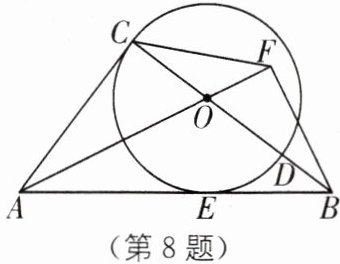
8. 方程思想 (2024·镇江期中)如图,点D是△ABC的边BC上一点,以CD为直径的⊙O切AB于点E,BF⊥AO交AO的延长线于点F,且∠FBC= ∠CAF.
(1)求证:AC是⊙O的切线;
(2)若AC= 6,BC= 8.
①求⊙O的半径;
②连接CF,求BF的长.

答案：
 
(1)
∵BF⊥AO,
∴∠BFO=90°.
∵∠FBC=∠CAF,∠COA=∠FOB,
∴∠ACO=∠BFO=90°,
∴OC⊥AC.
∵OC是⊙O的半径，
∴AC是⊙O的切线
(2)①在Rt△ABC中,
∵AC=6,BC=8,∠ACB=90°,
∴AB=√(AC²+BC²)=10.
连接OE,如图所示
∵AC与AE都为⊙O的切线,
∴AC=AE=6,
∴BE=AB−AE=4.
在Rt△BOE中,设OC=OE=r,则有OB=8−r,
由勾股定理,得(8−r)²=r²+4²,解得r=3,即⊙O的半径为3.
②延长AC、BF交于点G,如
图所示,
∵AF⊥BG,
∴∠AFG=∠AFB=90°.
∵AC与AE都为⊙O的切线,
∴OC⊥AC,OE⊥AE,
∠CAO=∠EAO.
在△AFG和△AFB中,
∠GAF=∠BAF,
AF=AF,
∠AFG=∠AFB=90°,
∴△AFG≌△AFB(ASA),
∴AG=AB=10,BF=GF,
∴CG=BE=4.
在Rt△BCG中,∠BCG=90°,则BG=√(BC²+CG²)=√(8²+4²)=4√5,
∴BF=1/2BG=2√5

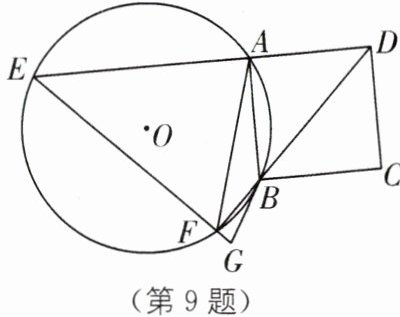
9. 如图,四边形ABCD是正方形,点A、点B在⊙O上,边DA的延长线交⊙O于点E,对角线DB的延长线交⊙O于点F,连接EF并延长至点G,使∠FBG= ∠FAB.
(1)求证:BG与⊙O相切;
(2)若⊙O的半径为1,求AF的长.

答案：
 
(1)如图,连接BE.
∵四边形ABCD是正方形,
∴∠BAD=90°,
∴∠BAE=90°,
∴BE是⊙O的直径
∵∠BAF+∠EAF=90°,∠EAF=∠EBF,
∠FBG=∠FAB,
∴∠FBG+∠EBF=90°,
∴∠OBG=90°.
∵OB为⊙O的半径,
∴BG与⊙O相切.
(2)如图,连接OA、OF,
∵四边形ABCD是正方形,BE是⊙O的直径，
∴∠EFD=90°.
∵∠FDE=45°,
∴∠FED=45°,
∴∠AOF=90°.
∵OA=OF=1,
∴在Rt△AOF中,AF²=AO²+FO²=1+1=2,
∴AF=√2.

10. 一题多问 (2025·南京联合体期末)借助运动的视角看图形变化是非常重要的数学眼光……
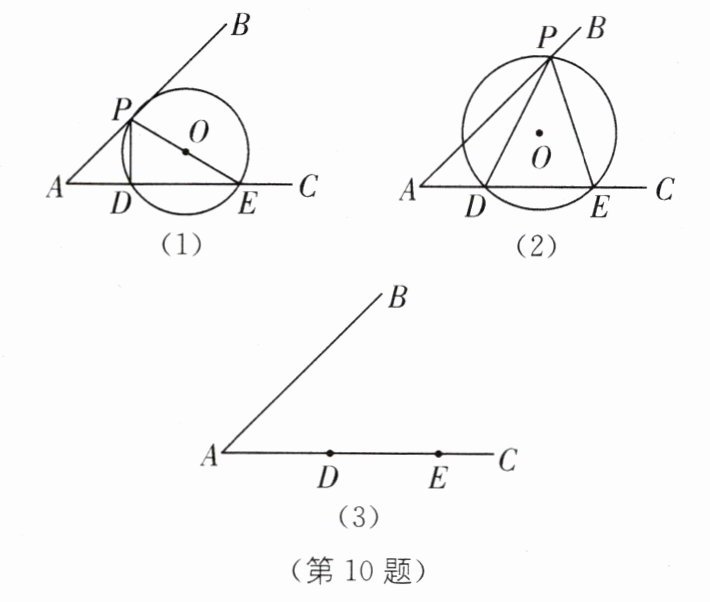
已知∠A= 45°,点D、E在AC上,DE= 10,点P在AB上,连接PD、PE,作△PDE的外接圆⊙O.
(1)当AD= 6时,
①如图(1),若PE是⊙O的直径,则⊙O的半径为______;
②如图(2),若AP= 12√2,求⊙O的半径.
(2)当AD= 10时,如图(3),若⊙O与AB相切于点P,用直尺和圆规作出点P的位置.
(要求:不写作法,保留作图痕迹,写出必要的文字说明)
(3)设AD= m,对于每一个m的值,⊙O的半径随着点P的位置的变化而变化,直接写出⊙O的半径的最小值及对应的m的取值范围(可用含m的式子表示).

答案：

(1)①√34　[解析]
∵作△PDE的外接圆⊙O,PE是直径,
∴PD⊥AE,即∠ADP=90°.
∵∠A=45°,
∴AD=PD=6.
∵DE=10,
∴由勾股定理得PE=√(PD²+DE²)=√(36 + 100)=2√34,
∴⊙O的半径为√34
②如图
(1),过点O、P作AC的垂线，垂足分别为G、F,
过点O作OH⊥PF,垂足为H,连接OP、OD.
∵PF⊥AF,AP=12√2,∠BAC=45°,
∴PF=AF=12,
∴DF=AF−AD=6,EF=AE−AF=4.
∵在⊙O中,OG⊥DE,
∴DG=EG=5.
∵∠OGF=∠GFH=∠OHF=90°,
∴四边形OGFH为矩形，
∴OH=GF=DF−DG=1,HF=OG.
设HF=OG=x,则PH=12−x,
在Rt△ODG和Rt△OHP中，由勾股定理，得OD²=OG²+DG²,OP²=OH²+PH²,
∴OG²+DG²=OH²+PH²,即x²+5²=1²+(12−x)²,
解得x=5,
∴OD=√(OG²+DG²)=5√2,即r=5√2
(2)如图
(2),作AE的垂直平分线交AB于点P,则点P 即为所求.
(3)如图
(3),以DE为直径的圆与AB相切时,OP=1/2DE=5,OP⊥AP,则OA=5√2,m=5√2−5.
①当0＜m≤5√2−5时,r=5;
②当m＞5√2−5时，易知当⊙O与AB相切时，半径最小,如图
(4),
设OP=OD=r,则OF=√2r,OG=m + 5 - √2r,
在Rt△OGD中,由勾股定理得OD²=OG²+DG²,
即r²=5²+(m + 5 - √2r)²,
解得r=√2(m + 5) - √(m² + 10m)
综上,当0＜m≤5√2−5时,r=5;当m＞5√2−5时,r=√2(m + 5) - √(m² + 10m).