《2025年实验班提优训练九年级数学上册苏科版》

11. 如图,在坐标平面上,A、B 两点分别为圆 P 与 x 轴、y 轴的交点,直线 l 过点 P 且与 AB 垂直,点 C 为 l 与 y 轴的交点. 若点 A、B、C 的坐标分别为(a,0)、(0,4)、(0,-5),其中 a＜0,则 a 的值为(A).
A.$-2\sqrt{14}$
B.$-2\sqrt{5}$
C.-8
D.-7

答案： A　[解析]连接AC,由题意,得BC=OB+OC=9.
∵直线l经过点P且与AB垂直,
∴直线l是线段AB的垂直平分线，
∴AC=BC=9.在Rt△AOC中,AO=$\sqrt{AC²−OC²}$=2$\sqrt{14}$.
∵a＜0,
∴a=−2$\sqrt{14}$.故选A

12. 如图,在 5×7 网格中,各小正方形边长均为 1,点 O、A、B、C、D、E 均在格点上,点 O 是△ABC 的外心,在不添加其他字母的情况下,则除△ABC 外把你认为外心也是 O 的三角形都写出来 △ABD、△ACD、△BCD.

答案： △ABD、△ACD、△BCD　[解析]由图,可得OA=OB=OC=OD=$\sqrt{1²+2²}$=$\sqrt{5}$，OE=$\sqrt{1²+3²}$=$\sqrt{10}$，
∴△ABD、△ACD、△BCD的外心均为点O 知识拓展　重心、外心、内心、垂心、旁心统称为三角形的“五心”。三角形的三条中线的交点叫三角形的重心，重心到顶点的距离与重心到对边中点的距离之比为2:1；三角形三边的垂直平分线的交点叫三角形的外心(外接圆的圆心)，外心到三角形三个顶点的距离相等；三角形的内心是三角形三条角平分线的交点(或内切圆的圆心)，内心到三角形三边的距离相等；三角形的一条内角平分线与其他两个角的外角平分线交于一点，该点即为三角形的旁心，旁心到三角形三边的距离相等；三角形的垂心是三角形三边上的高的交点。

13. (2025·苏州姑苏区振华中学期中)如图,在平面直角坐标系中,A(0,4)、B(4,4)、C(6,2).
(1)经过 A、B、C 三点的圆弧所在圆的圆心 M 的坐标为(2,0)；
(2)这个圆的半径为2$\sqrt{5}$；
(3)直接判断点 D(5,-2)与⊙M 的位置关系. 点 D(5,-2)在⊙M内(填“内”“外”或“上”).

答案：
(1)(2,0)
(2)2$\sqrt{5}$　[解析]
∵A(0,4),M(2,0),
∴MA=$\sqrt{2²+4²}$=2$\sqrt{5}$，即⊙M的半径为2$\sqrt{5}$
(3)内　[解析]
∵D(5,−2),M(2,0),
∴DM=$\sqrt{(5−2)²+2²}$=$\sqrt{13}$
∵$\sqrt{13}$＜2$\sqrt{5}$，
∴点D在⊙M内

14. (南京中华中学特长生)如图,∠ACB= 90°,△DEF 中,∠D= 90°,DE= 3,DF= 4,点 E、F 分别在射线 CB、CA 上滑动,开始时,点 F 与点 C 重合. 当点 E 向点 C 运动时,点 F 沿着 CA 方向运动(保持△DEF 形状不变),点 E 从起始位置运动到点 C 的过程中,点 D 的运动轨迹的长度是 .

答案：
2　[解析]在运动过程中,如图,作EF中点M,连接CM、DM、CD,由斜边中线可得CM=DM=$\frac{1}{2}$EF=$\frac{5}{2}$.
∵∠ECF=∠EDF=90°,
∴点C、E、D、F在以EF为直径的圆上,若四边形中有两个对角为90°则四边形可确定一个圆，且圆心为另一条对角线的中点当C、M、D共线时,CD最大值为CM+DM=5,当E与C重合时,CD最小值和ED相等,为3,
∴点D的运动轨迹(注意，不是路程)长度为5−3=2.

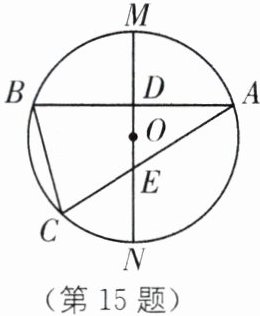
15. (2025·金华东阳期中改编)如图,已知△ABC 内接于⊙O,直径 MN⊥AB 于点 D,交 AC 于点 E,且 MD= DE. 若 MN= 3NE,且 AB= $4\sqrt{6}$,求 AE 的长.

答案：
如图,连接OA,设NE=x,则MN=3NE=3x,ME=2x.
∵MD=DE,
∴MD=DE=x.
∵MN是⊙O的直径,
∴OA=OM=$\frac{3}{2}$x,
∴OD=OM−MD=$\frac{1}{2}$x.
∵MN⊥AB于点D,
∴AD=BD=$\frac{1}{2}$AB=$\frac{1}{2}$×4$\sqrt{6}$=2$\sqrt{6}$在Rt△AOD中,AD²+OD²=OA²,
∴(2$\sqrt{6}$)²+($\frac{1}{2}$x)²=($\frac{3}{2}$x)²，解得x=2$\sqrt{3}$
∴DE=2$\sqrt{3}$.在Rt△AED中,AE=$\sqrt{DE²+AD²}$=$\sqrt{(2\sqrt{3})^{2}+(2\sqrt{6})^{2}}$=6.

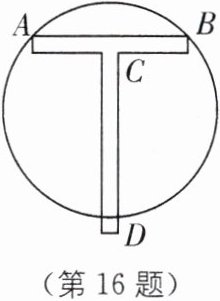
16. 教材 P52 练习 T1·变式 图中工具边 CD 所在的直线恰好垂直平分边 AB,你能利用这个工具找出一个圆的圆心吗？请说明理由.

答案： 把AB放于不同的位置，沿CD画直线，两直线的交点就是所求的圆心.理由:垂直平分圆上一弦的直线经过该圆的圆心.

17. 分类讨论思想 我们知道,到线段两端距离相等的点在线段的垂直平分线上. 由此,我们可以引入如下新定义：到三角形的两个顶点距离相等的点,叫做此三角形的准外心.
(1)如图(1),点 P 在线段 BC 上,∠ABP= ∠APD= ∠PCD= 90°,BP= CD,求证：点 P 是△APD 的准外心；
(2)如图(2),在 Rt△ABC 中,∠BAC= 90°,BC= 5,AB= 3,△ABC 的准外心 P 在△ABC 的直角边上,试求 AP 的长.

答案：

(1)
∵∠ABP=∠APD=∠PCD=90°,
∴∠APB+∠PAB=90°,∠APB+∠DPC=90°,
∴∠PAB=∠DPC.在△ABP和△PCD中,$\begin{cases}∠PAB = ∠DPC\\∠ABP = ∠PCD\\BP = CD\end{cases}$
∴△ABP≌△PCD(AAS),
∴AP=PD,
∴点P是△APD的准外心.
(2)
∵∠BAC=90°,BC=5,AB=3,
∴AC=$\sqrt{5²−3²}$=4.当点P在AB上,PA=PB时,AP=$\frac{1}{2}$AB=$\frac{3}{2}$;当点P在AC上,PA=PC时,AP=$\frac{1}{2}$AC=2;当点P在AC上,PB=PC时,如图, 设AP=t,则PC=PB=4−t,在Rt△ABP中,3²+t²=(4−t)²,解得t=$\frac{7}{8}$，即此时AP=$\frac{7}{8}$.综上所述，AP的长为$\frac{3}{2}$或2或$\frac{7}{8}$.