《2025年实验班提优训练九年级数学上册苏科版》

8. 跨学科 古诗词理解 《念奴娇·赤壁怀古》,在苏轼笔下,周瑜年少有为,文采风流,雄姿英发,谈笑间,樯橹灰飞烟灭,然天妒英才,英年早逝,欣赏下面改编的诗歌,“大江东去浪淘尽,千古风流数人物.而立之年督东吴,早逝英年两位数.十位恰小个位三,个位平方与寿符.”则这位风流人物去世的年龄为36岁.

答案： 36　[解析]设这位风流人物去世的年龄十位数字为x,则个位数字为x+3,则根据题意$10x+(x+3)=(x+3)^{2}$，整理得$x^{2}-5x+6=0$，解得$x_{1}=2,x_{2}=3$，由题意,而立之年督东吴,得x=2应舍去,
∴这位风流人物去世的年龄为36岁.

9.(2025·苏州太仓期末)某社区为了解决停车难的问题,计划将一块矩形空地ABCD改建成一个小型停车场,其中阴影部分为停车位区域,其余部分均为宽度是x米的道路,如图所示.已知AD= 50米,AB= 32米,且停车区域(即阴影部分)的面积为880平方米,求道路的宽度x.

答案： 由题意,得$(50-x)(32-2x)=880$，整理,得$x^{2}-66x+360=0$，解得$x_{1}=60$(不合题意,舍去),$x_{2}=6$.故道路的宽度x是6米.

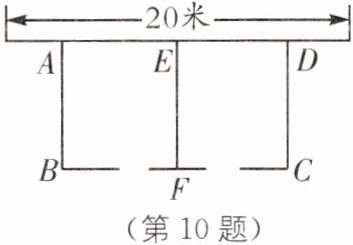
10.(2025·扬州期末)如图,利用一面墙(墙的长度为20米),用34米长的篱笆围成两个长方形鸡场.中间用一道篱笆隔开,每个鸡场均留一道1米宽的门,两个鸡场总面积为96平方米,求AB的长.

答案： 设AB的长为x米,则BC=BF+CF=34−3x+2=(36−3x)米,根据题意,得$x(36-3x)=96$，解得x=4或x=8.当x=4时,BC=36−3x=24＞20，
∴x=4不合题意.故x的值为8,即AB的长为8米.

11. 教材P24问题1·变式 将一条长为20cm的铁丝剪成两段,并以每一段铁丝的长度为周长做成一个正方形.
(1)要使这两个正方形的面积之和等于$17cm^2,$那么这段铁丝剪成两段后的长度分别是多少?
(2)两个正方形的面积之和可能等于$12cm^2$吗?若能,求出两段铁丝的长度;若不能,请说明理由.

答案：
(1)设剪成两段后其中一段长为xcm，则另一段长为(20−x)cm.由题意,得$(\frac {x}{4})^{2}+(\frac {20-x}{4})^{2}=17$，解得$x_{1}=16,x_{2}=4$，当x=16时,20−x=4;当x=4时,20−x=16.
∴这段铁丝剪成两段后的长度分别是16cm和4cm.
(2)不能.理由如下:假设能等于12,得$(\frac {x}{4})^{2}+(\frac {20-x}{4})^{2}=12$，整理,得$x^{2}-20x+104=0$.
∵$\Delta =(-20)^{2}-4×104=-16＜0$，
∴此方程无解，即不能剪成两段使得围成的两个正方形的面积之和等于12cm².

12. 新情境 建设美丽乡村 某驻村工作队,为带动群众增收致富,巩固脱贫攻坚成效,决定在该村山脚下,围一块面积为$600m^2$的矩形试验茶园,便于成功后大面积推广.如图所示,茶园一面靠墙,墙长35m,另外三面用69m长的篱笆围成,其中一边开有一扇1m宽的门(不包括篱笆).求这个茶园的长和宽.

答案： 设茶园垂直于墙的一边长为xm，根据题意,得$x(69+1-2x)=600$，整理,得$x^{2}-35x+300=0$，解得$x_{1}=15,x_{2}=20$.当x=15时,70−2x=40＞35,不符合题意，舍去；当x=20时,70−2x=30,符合题意.故这个茶园的长和宽分别为30m、20m.
易错警示　设茶园垂直于墙的一边长为xm时,另一边的长度为(69+1−2x)m,而不是(69−2x)m或(69−1-2x)m.