第110页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
7. 实验班原创 某校气象兴趣小组的同学们想预估一下南京市 2025 年 10 月份日平均气温状况. 他们收集了南京市近五年 10 月份每天的日平均气温,从中随机抽取了 60 天的日平均气温,并绘制成如下统计图:
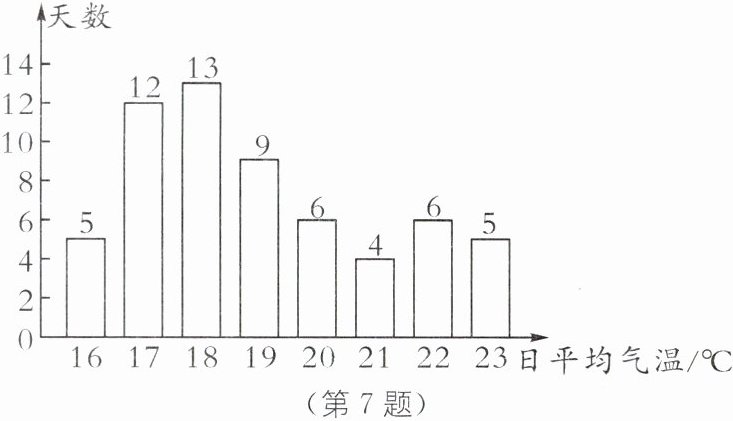
根据以上信息,回答下列问题:
(1)这 60 天的日平均气温的平均数为
(2)若日平均气温在 18°C~21°C 的范围内(包含 18°C 和 21°C)为"舒适温度",请预估南京市 2025 年 10 月份日平均气温为"舒适温度"的天数.

根据以上信息,回答下列问题:
(1)这 60 天的日平均气温的平均数为
$19^{\circ }C$
,中位数为$18.5^{\circ }C$
,众数为$18^{\circ }C$
;(2)若日平均气温在 18°C~21°C 的范围内(包含 18°C 和 21°C)为"舒适温度",请预估南京市 2025 年 10 月份日平均气温为"舒适温度"的天数.
$\because \frac{13 + 9 + 6 + 4}{60}×31\approx17$(天),
∴估计南京市 2025 年 10 月份日平均气温为"舒适温度"的天数为 17 天.
∴估计南京市 2025 年 10 月份日平均气温为"舒适温度"的天数为 17 天.
答案:
(1)$19^{\circ }C$ $18.5^{\circ }C$ $18^{\circ }C$;
(2)$\because \frac{13 + 9 + 6 + 4}{60}×31\approx17$(天),
∴估计南京市 2025 年 10 月份日平均气温为"舒适温度"的天数为 17 天.
(1)$19^{\circ }C$ $18.5^{\circ }C$ $18^{\circ }C$;
(2)$\because \frac{13 + 9 + 6 + 4}{60}×31\approx17$(天),
∴估计南京市 2025 年 10 月份日平均气温为"舒适温度"的天数为 17 天.
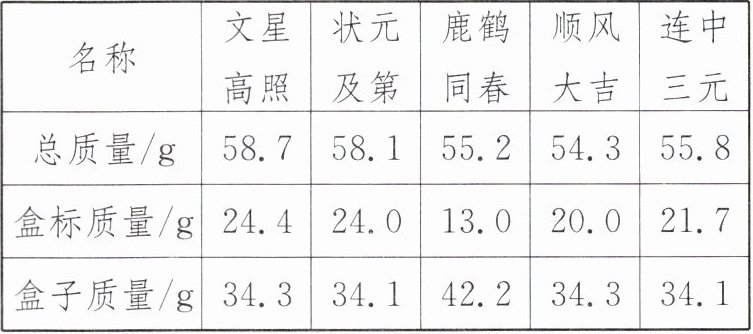
8. 传统文化 古钱币 如图,下列装在相同的透明密封盒内的古钱币,其密封盒上分别标有古钱币的尺寸及质量,例如:钱币"文星高照"密封盒上所标"45.4*2.8 mm,24.4g"是指该枚古钱币的直径为 45.4 mm,厚度为 2.8 mm,质量为 24.4 g. 已知这些古钱币的材质相同.
45.4*2.8mm,24.4g 48.1*2.4mm,24.0g 45.1*2.3mm,13.0g

文星高照
状元及第
鹿鹤同春
44.6*2.1mm,20.0g 45.5*2.3mm,21.7g
顺风大吉
连中三元
根据图中信息,解决下列问题:
(1)这 5 枚古钱币,所标直径的平均数是______mm,所标厚度的众数是______mm,所标质量的中位数是______g;
(2)由于古钱币无法从密封盒内取出,为判断密封盒上所标古钱币的质量是否有错,桐桐用电子秤测得每枚古钱币与其密封盒的总质量如下:
|名称|文星高照|状元及第|鹿鹤同春|顺风大吉|连中三元|
|总质量/g|58.7|58.1|55.2|54.3|55.8|
|盒标质量/g|24.4|24.0|13.0|20.0|21.7|
|盒子质量/g|34.3|34.1|42.2|34.3|34.1|
请你应用所学的统计知识,判断哪枚古钱币所标的质量有错,并计算该枚古钱币的实际质量约为多少克.
(1)
(2)
45.4*2.8mm,24.4g 48.1*2.4mm,24.0g 45.1*2.3mm,13.0g

文星高照
状元及第
鹿鹤同春
44.6*2.1mm,20.0g 45.5*2.3mm,21.7g

顺风大吉
连中三元
根据图中信息,解决下列问题:
(1)这 5 枚古钱币,所标直径的平均数是______mm,所标厚度的众数是______mm,所标质量的中位数是______g;
(2)由于古钱币无法从密封盒内取出,为判断密封盒上所标古钱币的质量是否有错,桐桐用电子秤测得每枚古钱币与其密封盒的总质量如下:
|名称|文星高照|状元及第|鹿鹤同春|顺风大吉|连中三元|
|总质量/g|58.7|58.1|55.2|54.3|55.8|
|盒标质量/g|24.4|24.0|13.0|20.0|21.7|
|盒子质量/g|34.3|34.1|42.2|34.3|34.1|
请你应用所学的统计知识,判断哪枚古钱币所标的质量有错,并计算该枚古钱币的实际质量约为多少克.
(1)
45.74
2.3
21.7
;(2)
“鹿鹤同春”密封盒的质量异常,故“鹿鹤同春”的质量与实际质量差异较大,其余四个盒子的质量的平均数为$\frac{34.3 + 34.1 + 34.3 + 34.1}{4}=34.2(g)$,55.2 - 34.2 = 21.0(g).故“鹿鹤同春”的实际质量约为 21.0 克.
答案:
(1)45.74 2.3 21.7;
(2)“鹿鹤同春”密封盒的质量异常,故“鹿鹤同春”的质量与实际质量差异较大,其余四个盒子的质量的平均数为$\frac{34.3 + 34.1 + 34.3 + 34.1}{4}=34.2(g)$,55.2 - 34.2 = 21.0(g).故“鹿鹤同春”的实际质量约为 21.0 克.
(1)45.74 2.3 21.7;
(2)“鹿鹤同春”密封盒的质量异常,故“鹿鹤同春”的质量与实际质量差异较大,其余四个盒子的质量的平均数为$\frac{34.3 + 34.1 + 34.3 + 34.1}{4}=34.2(g)$,55.2 - 34.2 = 21.0(g).故“鹿鹤同春”的实际质量约为 21.0 克.
查看更多完整答案,请扫码查看


