《2025年实验班提优训练九年级数学上册苏科版》

15. 中考新考法 满足结论的条件开放 如图(1),在$\odot O$中,弦 CD 垂直直径 AB 于点 E,已知$AC= 6$,$DB= 4$.
(1)求直径 AB 的长.
(2)小慧说“若将题目条件中的‘直径 AB’改为‘弦 AB’,其余条件均不变(如图(2)),$\odot O$的直径仍不变”,你觉得小慧的说法正确吗？请说明理由.

答案：
(1)连接AD，如图
(1)所示.
∵AB为直径，
∴∠ADB = 90°.
∵弦CD垂直于直径AB于点E，
∴由垂径定理可知AD = AC = 6.在Rt△ADB中，AB = √(AD² + DB²)=√(6² + 4²)=2√13.故直径AB的长为2√13.
(2)小慧的说法正确，理由如下:连接AO，并延长AO交⊙O于点F，连接CF，如图
(2)所示.
∵AF为直径，
∴∠ACF = 90°，即∠ACD + ∠FCD = 90°.
∵AB⊥CD，
∴∠EBD + ∠BDE = 90°.
∵∠DBE = ∠ACD，
∴∠FCD = ∠BDE，
∴$\overset{\frown}{DF}=\overset{\frown}{BC}$，
∴$\overset{\frown}{CF}=\overset{\frown}{DB}$，
∴CF = BD = 4.在Rt△ACF中，AF = √(AC² + CF²)=√(6² + 4²)=2√13.
∴⊙O的直径不变.

16. 如图,在$\odot O$中,弦 AB、CD 互相垂直,垂足为点 M,点 F 是$\overset{\frown}{BD}$上的一点,且$\overset{\frown}{BF}= \overset{\frown}{BC}$,AF 分别与 CD、BD 相交于点 E、N,连接 FD、MN.

(1)求证：$DE= DF$；
(2)若$\odot O$的半径为 8,$\angle BAF= 22.5^{\circ}$,求线段 MN 的长.

答案：
(1)
∵$\overset{\frown}{BF}=\overset{\frown}{BC}$，
∴∠BAF = ∠BDC.
∵AB⊥CD，
∴∠BAF + ∠AEC = 90°，∠B + ∠BDC = 90°，
∴∠AEC = ∠B.
∵∠AEC = ∠DEF，∠B = ∠F，
∴∠DEF = ∠F，
∴DE = DF.
(2)如图，连接AC、FC、OC、OF.
∵BF = BC，
∴∠BDC = ∠BDF.
∵DE = DF，
∴EN = NF.
∵∠ACD = ∠B，∠AEC = ∠B，
∴∠ACD = ∠AEC，
∴AE = AC.
∵AB⊥CD，
∴EM = MC，
∴MN = 1/2CF.
∵∠BAF = 22.5°，
∴∠CDF = 2∠BAF = 45°，
∴∠COF = 2∠CDF = 90°，
∴FC = 8√2，
∴MN = 4√2.

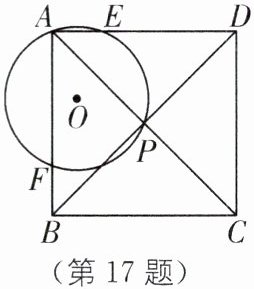
17. 四点共圆模型 (湖北黄冈中学自主招生)如图,四边形 ABCD 为正方形,$\odot O$过正方形的顶点 A 和对角线的交点 P,分别交 AB、AD 于点 F、E.
(1)求证：$DE= AF$；
(2)若$\odot O的半径为\frac{\sqrt{3}}{2}$,$AB= \sqrt{2}+1$,求$\frac{AE}{ED}$的值.

精题详解

答案：
(1)连接EP、FP，如图.
∵四边形ABCD为正方形，
∴∠BAD = 90°，∠BPA = 90°，PA = PB，
∴∠FPE = 90°，
∴∠BPF = ∠APE.
∵∠FBP = ∠PAE = 45°，
∴△BPF≌△APE(ASA)，
∴BF = AE，而AB = AD，
∴DE = AF.
(2)如图，连接EF.
∵∠BAD = 90°，
∴EF为⊙O的直径，而⊙O的半径为√3/2，
∴EF = √3，
∴AF² + AE² = EF² = (√3)² = 3，而DE = AF，
∴DE² + AE² = 3①.
∵AD = AE + ED = AB，
∴AE + ED = √2 + 1②，由①②联立起来组成方程组，解得AE = 1，ED = √2或AE = √2，ED = 1，
∴AE/ED = √2/2或√2.

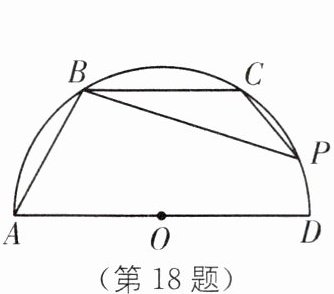
18. (2024·海南中考)如图,AD 是半圆 O 的直径,点 B、C 在半圆上,且$\overset{\frown}{AB}= \overset{\frown}{BC}= \overset{\frown}{CD}$,点 P 在$\overset{\frown}{CD}$上,若$\angle PCB= 130^{\circ}$,则$\angle PBA$等于(B).

A.$105^{\circ}$
B.$100^{\circ}$
C.$90^{\circ}$
D.$70^{\circ}$

答案： B [解析]如图，连接OB、OC、OP.
∵AD是半圆O的直径，
∴∠AOD = 180°.
∵$\overset{\frown}{AB}=\overset{\frown}{BC}=\overset{\frown}{CD}$，
∴∠AOB = ∠BOC = ∠COD = 60°.
∵OA = OB = OC，
∴△AOB、△BOC均是等边三角形，
∴∠ABO = ∠CBO = ∠BCO = 60°，
∴∠ABC = ∠ABO + ∠CBO = 120°.
∵OC = OP，∠PCB = 130°，
∴∠OPC = ∠OCP = ∠PCB - ∠BCO = 130° - 60° = 70°，
∴∠COP = 180° - ∠OPC - ∠OCP = 180° - 70° - 70° = 40°，
∴∠PBC = 1/2∠COP = 1/2×40° = 20°，
∴∠PBA = ∠ABC - ∠PBC = 120° - 20° = 100°.故选B.

19. (2024·滨州中考)如图,四边形 ABCD 内接于$\odot O$,若四边形 OABC 是菱形,则$\angle D= $60°.

答案： 60 [解析]
∵四边形ABCD内接于⊙O，
∴∠B + ∠D = 180°.
∵四边形OABC是菱形，
∴∠B = ∠AOC，
∴∠AOC + ∠D = 180°.由圆周角定理得∠D = 1/2∠AOC，
∴2∠D + ∠D = 180°，
∴∠D = 60°.