《2025年实验班提优训练九年级数学上册苏科版》

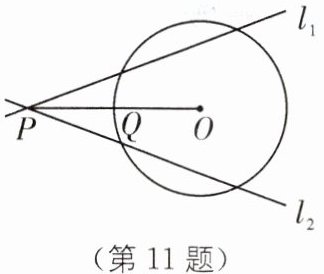
11. 如图,点 P 为$\odot O$外一点,连接 OP 交$\odot O$于点 Q,且$PQ= OQ$,经过点 P 的直线$l_{1}$、$l_{2}都与\odot O$有公共点,则$l_{1}与l_{2}$所成的锐角α的取值范围是( ).

A.$0^{\circ }＜α≤30^{\circ }$
B.$0^{\circ }＜α≤45^{\circ }$
C.$0^{\circ }＜α≤60^{\circ }$
D.$0^{\circ }＜α≤90^{\circ }$

答案：
C　[解析]如图,当直线l₁、l₂都与⊙O相切时,切点分别为A、B,连接OA,则OA⊥l₁.
∵OA = OQ = PQ,
∴OA = (1/2)OP,
∴∠OPA = 30°.同理,∠OPB = 30°,
∴l₁与l₂所成的锐角α的取值范围是0°＜α≤60°.故选C.

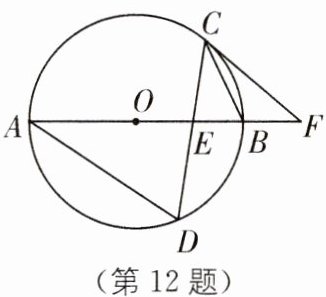
12. 如图,在$\odot O$中,直径 AB 与弦 CD 相交于点 E,连接 BC、AD,过点 C 的切线与 AB 的延长线交于点 F,若$∠D= 65^{\circ }$,则$∠F$的度数等于(C).

A.$30^{\circ }$
B.$35^{\circ }$
C.$40^{\circ }$
D.$45^{\circ }$
]

答案： C　[解析]连接OC,
∵CF是⊙O的切线,
∴∠OCF = 90°,由圆周角定理,得∠ABC = ∠D = 65°.
∵OC = OB,
∴∠OCB = ∠ABC = 65°,
∴∠BOC = 180° - 65° - 65° = 50°,
∴∠F = 90° - ∠BOC = 40°.故选C.

13.(2025·宿迁宿豫区期中)如图,$∠BAC= 45^{\circ }$,点 O 在 AC 上,且$AO= 4$,以点 O 为圆心,r 为半径画圆,若$∠BAC$的边 AB 与$\odot O$有两个公共点,则 r 的取值范围为______.

答案：
2√2＜r≤4　[解析]如图
(1),根据等腰直角三角形的性质,求得圆心到直线AB的距离是OD = 2√2.若AB与⊙O相切,则此时圆的半径是2√2；如图
(2),当⊙O经过点A时,r = 4,则当r＞4时,⊙O与AB只有一个交点,切勿漏掉过端点的情况.故∠BAC的边AB与⊙O有两个公共点时,则r的取值范围是2√2＜r≤4.

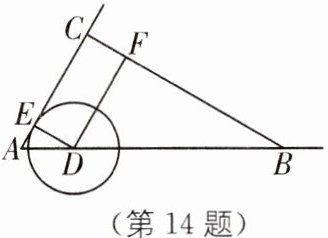
14.(2024·镇江期中)在$Rt\triangle ABC$中,$∠ACB= 90^{\circ },∠A= 60^{\circ },AB= 10cm$,点 D 从点 A 出发,沿射线 AB 以 2 cm/s 的速度移动,移动过程中始终保持$DE// BC,DF// AC$(点 E、F 分别在射线 AC、CB 上).以点 D 为圆心,DE 为半径作$\odot D$,若$\odot D$上恰好只有两个点到直线 BC 的距离为 3 cm,设点 D 移动的时间为 t 秒,则 t 的取值范围是______.
]

答案：
√3 - 1＜t＜4√3 - 4
[解析]如图,设直线GH和MN到BC的距离为3cm,
∴GH//BC//MN,CG = CM = 3cm.
∵∠ACB = 90°,∠A = 60°,
∴∠ABC = 30°,
∴AC = ($\frac{1}{2}$)AB = 5cm.
∵AD = 2t cm,
∴AE = ($\frac{1}{2}$)AD = t cm,
∴DE = √(AD² - AE²) = √3t cm.根据题意,得①当点D在边AB上时,⊙D与GH相切,⊙D恰好有一个点到BC的距离为3cm,
∵AE = t cm,AC = 5cm,
∴CE = (5 - t)cm = DF,
∴DF - DE＜3,即|5 - t - √3t|＜3,
∴t＞√3 - 1.②当⊙D与MN相切时,⊙D与BC有2个交点,
∴DE - DF＜3即√3t - 5 + t＜3,
∴t＜4√3 - 4,
∴√3 - 1＜t＜4√3 - 4.

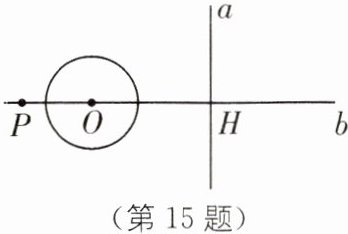
15. 分类讨论思想 (2025·盐城阜宁期中)如图,直线$a⊥b$,垂足为 H,点 P 在直线 b 上,$PH= 6cm$,O 为直线 b 上一动点,若以 2 cm 为半径的$\odot O$与直线 a 相切,则 OP 的长为______.

答案：
4cm或8cm　[解析]
∵直线a⊥b,O为直线b上一动点,
∴⊙O与直线a相切时,切点为H,
∴OH = 2cm.当点O在点H的左侧,⊙O与直线a相切时,如图
(1)所示,OP = PH - OH = 6 - 2 = 4(cm)；当点O在点H的右侧,⊙O与直线a相切时,如图
(2)所示,OP = PH + OH = 6 + 2 = 8(cm)；
∴⊙O与直线a相切,OP的长为4cm或8cm.

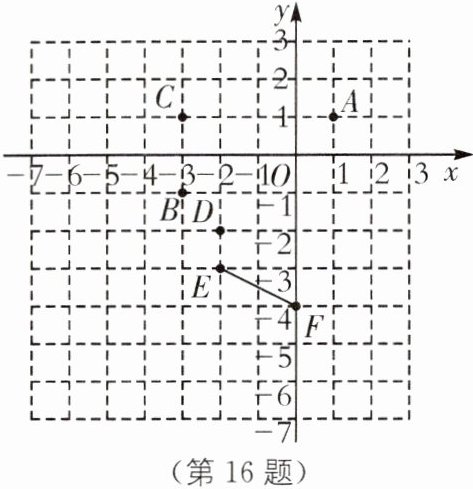
16.(2024·镇江润州区期中)如图,在同一平面直角坐标系中有 6 个点:$A(1,1)$、$B(-3,-1)$、$C(-3,1)$、$D(-2,-2)$、$E(-2,-3)$、$F(0,-4)$.
(1)$\triangle ABC$的外接圆圆心点 P 的坐标为______,半径是______;
(2)若将直线 EF 沿 y 轴向上平移,当它经过点 D 时,此时的直线为$l_{1}与\odot P$的位置关系是______.
]

答案：

(1)(-1,0) √5　[解析]画出△ABC的外接圆⊙P,如图所示,则P(-1,0),半径PA = √[(-1 - 1)² + 1²] = √5.
(2)相切　[解析]设直线EF解析式为y = kx + b,把E和F坐标代入,得{-2k + b = -3,b = -4},解得{k = -(1/2),b = -4},
∴直线EF解析式为y = -(1/2)x - 4.由平移性质及题意,得直线l₁的解析式为y = -(1/2)x - 4 + 1,即y = -(1/2)x - 3.由面积法可得圆心P(-1,0)到直线的距离d = √5 = r,
∴直线l₁与⊙P相切.

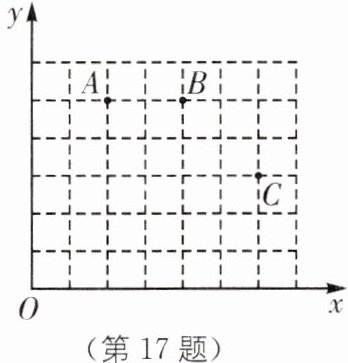
17.(2025·宿迁宿城区期中)如图,在平面直角坐标系中,$A(2,5),B(4,5),C(6,3),\odot M$经过 A、B、C 三点.
(1)点 M 的坐标是______;
(2)判断$\odot M$与 y 轴的位置关系,并说明理由.
]

答案：

(1)(3,2)　[解析]连接AB、BC,分别作AB、BC的垂直平分线交于点M,则以点M为圆心,以AM为半径的圆为所求,如图所示.根据网格的特征可得点M的坐标为(3,2).
(2)⊙M与y轴相交,理由如下:由勾股定理,得MA = √(1² + 3²) = √10,即⊙M的半径为r = √10.
∵⊙M的圆心M的坐标为(3,2),
∴点M到y轴的距离d = 3.
∵d＜r,
∴⊙M与y轴相交.