第90页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
17.(南京二十九中特长生)在$\triangle ABC$中,$AB= 2\sqrt{3}$,$60^{\circ}\leq\angle C\leq120^{\circ}$,求所有点 C 形成的图形的面积.
答案:
如图,点C所形成的图形为阴影部分的2倍(下面对称部分也对),易得OA=OB=OP=2,∠AOB=120°,
∵$\overset{\frown}{AmB}$在⊙O上,
∴PA=PB=2,∠APB=120°.
∵$\overset{\frown}{AOB}$在⊙P上,
∴$\overset{\frown}{AmB}$与$\overset{\frown}{AOB}$围成部分为所求图形,
∴S阴影=S扇形OAB + S△OAB + S△PAB - S扇形PAB=$\frac{240}{360}\pi×2^{2}+\frac{1}{2}×2\sqrt{3}×2-\frac{120}{360}\pi×2^{2}=\frac{4}{3}\pi+2\sqrt{3}$,
∴所有点C形成的图形的面积为$\frac{8}{3}\pi+4\sqrt{3}$.
如图,点C所形成的图形为阴影部分的2倍(下面对称部分也对),易得OA=OB=OP=2,∠AOB=120°,
∵$\overset{\frown}{AmB}$在⊙O上,
∴PA=PB=2,∠APB=120°.
∵$\overset{\frown}{AOB}$在⊙P上,
∴$\overset{\frown}{AmB}$与$\overset{\frown}{AOB}$围成部分为所求图形,
∴S阴影=S扇形OAB + S△OAB + S△PAB - S扇形PAB=$\frac{240}{360}\pi×2^{2}+\frac{1}{2}×2\sqrt{3}×2-\frac{120}{360}\pi×2^{2}=\frac{4}{3}\pi+2\sqrt{3}$,
∴所有点C形成的图形的面积为$\frac{8}{3}\pi+4\sqrt{3}$.

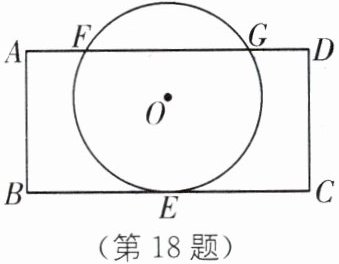
18. 分类讨论思想 (南京十三中特长生)四边形 ABCD 是矩形,$\odot O$与 BC 相切于点 E,且 E 为 BC 的中点,$AB= 3$,$BC= 6$,$AF= 3-\sqrt{3}$.
(1)求$\odot O$的半径.
(2)若矩形 ABCD 绕点 E 顺时针旋转$\alpha^{\circ}(0<\alpha\leq180)$,是否存在$\odot O$与矩形的一边相切?若存在,求出旋转角;若不存在,说明理由.
(3)以矩形 ABCD 为侧面围成圆柱,体积为$V_1$,连接 OF、OG,以扇形 OFG 为侧面围成锥形,体积为$V_2$,求$\frac{V_1}{V_2}$.
(1)求$\odot O$的半径.
(2)若矩形 ABCD 绕点 E 顺时针旋转$\alpha^{\circ}(0<\alpha\leq180)$,是否存在$\odot O$与矩形的一边相切?若存在,求出旋转角;若不存在,说明理由.
(3)以矩形 ABCD 为侧面围成圆柱,体积为$V_1$,连接 OF、OG,以扇形 OFG 为侧面围成锥形,体积为$V_2$,求$\frac{V_1}{V_2}$.

答案:
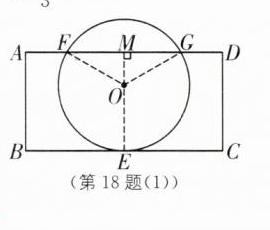
(1)如图
(1),连接OF、OG,连接EO并延长交FG于点M.
设⊙O的半径为r,则OE=OF=OG=r,OM⊥FG,
由切线的性质得OE⊥BC,由平行线的性质得OM⊥FG,OM=3-r,AM=BE=3,
∴FM=AM - AF=$\sqrt{3}$.
在Rt△OFM中,(3-r)²+($\sqrt{3}$)²=r²,
解得r=2,
∴⊙O的半径为2.
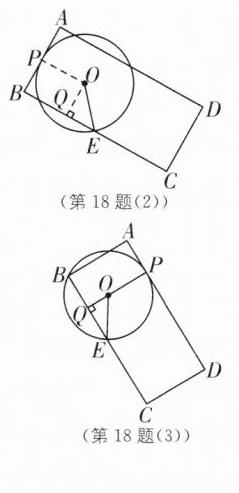
(2)如图
(2),当AB与⊙O相切时,
设切点为P,则OP=OE=2,BE=3.
过点O作OQ⊥BE,垂足为Q,则BQ=2,EQ=1,
∴∠OEQ=60°,
∴α=30°.
如图
(3),当AD与⊙O相切时,
同理OQ=1,OE=2,∠OEB=30°,
∴α=60°.
当α=180°时,BC与⊙O相切.
综上所述,α=30°、60°或180°.
(3)由
(1)得∠FOG=120°,$\overset{\frown}{FG}=\frac{120\pi×2}{180}=\frac{4}{3}\pi$,
∴圆锥底面半径$r_{2}=\frac{\frac{4}{3}\pi}{2\pi}=\frac{2}{3}$,圆锥底面圆的周长即为侧面扇形的弧长.
∴圆锥的高$h_{2}=\sqrt{2^{2}-(\frac{2}{3})^{2}}=\frac{4\sqrt{2}}{3}$,
∴$V_{2}=\frac{1}{3}\pi r_{2}^{2}h_{2}=\frac{1}{3}\pi×(\frac{2}{3})^{2}×\frac{4\sqrt{2}}{3}=\frac{16\sqrt{2}}{81}\pi$.
圆柱若以AB为高,则底面半径$r_{1}=\frac{6}{2\pi}=\frac{3}{\pi}$,
则$V_{1}=\pi r_{1}^{2}×3=\pi×(\frac{3}{\pi})^{2}×3=\frac{27}{\pi}$,
∴$\frac{V_{1}}{V_{2}}=\frac{\frac{27}{\pi}}{\frac{16\sqrt{2}}{81}\pi}=\frac{2187\sqrt{2}}{32\pi^{2}}$;
圆柱若以AD为高,则底面半径$r_{1}=\frac{3}{2\pi}$,则$V_{1}=\pi r_{1}^{2}×6=\pi×(\frac{3}{2\pi})^{2}×6=\frac{27}{2\pi}$,
∴$\frac{V_{1}}{V_{2}}=\frac{\frac{27}{2\pi}}{\frac{16\sqrt{2}}{81}\pi}=\frac{2187\sqrt{2}}{64\pi^{2}}$.
综上所述,$\frac{V_{1}}{V_{2}}$的值为$\frac{2187\sqrt{2}}{32\pi^{2}}$或$\frac{2187\sqrt{2}}{64\pi^{2}}$.


(1)如图
(1),连接OF、OG,连接EO并延长交FG于点M.
设⊙O的半径为r,则OE=OF=OG=r,OM⊥FG,
由切线的性质得OE⊥BC,由平行线的性质得OM⊥FG,OM=3-r,AM=BE=3,
∴FM=AM - AF=$\sqrt{3}$.
在Rt△OFM中,(3-r)²+($\sqrt{3}$)²=r²,
解得r=2,
∴⊙O的半径为2.
(2)如图
(2),当AB与⊙O相切时,
设切点为P,则OP=OE=2,BE=3.
过点O作OQ⊥BE,垂足为Q,则BQ=2,EQ=1,
∴∠OEQ=60°,
∴α=30°.
如图
(3),当AD与⊙O相切时,
同理OQ=1,OE=2,∠OEB=30°,
∴α=60°.
当α=180°时,BC与⊙O相切.
综上所述,α=30°、60°或180°.
(3)由
(1)得∠FOG=120°,$\overset{\frown}{FG}=\frac{120\pi×2}{180}=\frac{4}{3}\pi$,
∴圆锥底面半径$r_{2}=\frac{\frac{4}{3}\pi}{2\pi}=\frac{2}{3}$,圆锥底面圆的周长即为侧面扇形的弧长.
∴圆锥的高$h_{2}=\sqrt{2^{2}-(\frac{2}{3})^{2}}=\frac{4\sqrt{2}}{3}$,
∴$V_{2}=\frac{1}{3}\pi r_{2}^{2}h_{2}=\frac{1}{3}\pi×(\frac{2}{3})^{2}×\frac{4\sqrt{2}}{3}=\frac{16\sqrt{2}}{81}\pi$.
圆柱若以AB为高,则底面半径$r_{1}=\frac{6}{2\pi}=\frac{3}{\pi}$,
则$V_{1}=\pi r_{1}^{2}×3=\pi×(\frac{3}{\pi})^{2}×3=\frac{27}{\pi}$,
∴$\frac{V_{1}}{V_{2}}=\frac{\frac{27}{\pi}}{\frac{16\sqrt{2}}{81}\pi}=\frac{2187\sqrt{2}}{32\pi^{2}}$;
圆柱若以AD为高,则底面半径$r_{1}=\frac{3}{2\pi}$,则$V_{1}=\pi r_{1}^{2}×6=\pi×(\frac{3}{2\pi})^{2}×6=\frac{27}{2\pi}$,
∴$\frac{V_{1}}{V_{2}}=\frac{\frac{27}{2\pi}}{\frac{16\sqrt{2}}{81}\pi}=\frac{2187\sqrt{2}}{64\pi^{2}}$.
综上所述,$\frac{V_{1}}{V_{2}}$的值为$\frac{2187\sqrt{2}}{32\pi^{2}}$或$\frac{2187\sqrt{2}}{64\pi^{2}}$.
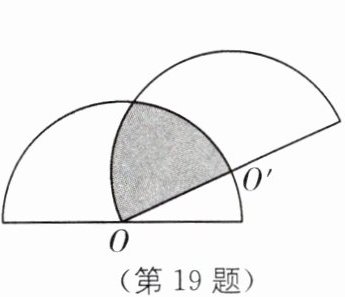
19.(2024·泰安中考)两个半径相等的半圆按如图方式放置,半圆$O'$的一个直径端点与半圆 O 的圆心重合,若半圆的半径为 2,则阴影部分的面积是( ).
A.$\frac{4}{3}\pi-\sqrt{3}$
B.$\frac{4}{3}\pi$
C.$\frac{2}{3}\pi-\sqrt{3}$
D.$\frac{4}{3}\pi-\frac{\sqrt{3}}{4}$

A.$\frac{4}{3}\pi-\sqrt{3}$
B.$\frac{4}{3}\pi$
C.$\frac{2}{3}\pi-\sqrt{3}$
D.$\frac{4}{3}\pi-\frac{\sqrt{3}}{4}$
答案:
A [解析]如图,连接OA、AO',作AB⊥OO'于点B.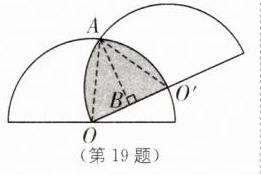
∵OA=OO'=AO'=2,
∴三角形AOO'是等边三角形,
∴∠AO O'=60°,OB=$\frac{1}{2}OO'=1$,
∴AB=$\sqrt{2^{2}-1^{2}}=\sqrt{3}$,
∴S弓形AO'=S扇形AO'O - S△AO'O=$\frac{60\pi×2^{2}}{360}-2×\sqrt{3}×\frac{1}{2}=\frac{2\pi}{3}-\sqrt{3}$,
∴S阴影=S弓形AO' + S扇形AOO'=$\frac{2\pi}{3}-\sqrt{3}+\frac{2\pi}{3}=\frac{4\pi}{3}-\sqrt{3}$.故选A.
A [解析]如图,连接OA、AO',作AB⊥OO'于点B.

∵OA=OO'=AO'=2,
∴三角形AOO'是等边三角形,
∴∠AO O'=60°,OB=$\frac{1}{2}OO'=1$,
∴AB=$\sqrt{2^{2}-1^{2}}=\sqrt{3}$,
∴S弓形AO'=S扇形AO'O - S△AO'O=$\frac{60\pi×2^{2}}{360}-2×\sqrt{3}×\frac{1}{2}=\frac{2\pi}{3}-\sqrt{3}$,
∴S阴影=S弓形AO' + S扇形AOO'=$\frac{2\pi}{3}-\sqrt{3}+\frac{2\pi}{3}=\frac{4\pi}{3}-\sqrt{3}$.故选A.
20. 新情境 实现共同富裕 (2024·内蒙古中考)为了促进城乡协调发展,实现共同富裕,某乡镇计划修建公路.如图,$\overset{\frown}{AB}与\overset{\frown}{CD}$是公路弯道的外、内侧边线,它们有共同的圆心 O,所对的圆心角都是$72^{\circ}$,点 A、C、O 在同一条直线上,公路弯道外侧边线比内侧边线多 36 米,则公路宽 AC 的长是______米.($\pi$取 3.14,计算结果精确到 0.1)


28.7
答案:
28.7 [解析]由题意,得$\frac{72\pi\cdot OA}{180}-\frac{72\pi\cdot OC}{180}=36$,
∴OA - OC=$\frac{90}{\pi}\approx28.7$(米).
∴AC=OA - OC=28.7米.
∴OA - OC=$\frac{90}{\pi}\approx28.7$(米).
∴AC=OA - OC=28.7米.
查看更多完整答案,请扫码查看


