第73页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
1. 教材 P74 习题 T12·变式 (2024·无锡江阴期中)如图,PA、PB 是$\odot O$的切线,切点分别为 A、B,点 C 在$\odot O$上,过点 C 的切线分别交 PA、PB 于点 D、E,若$PA= 1$,则$\triangle PDE$的周长为(

A.$\sqrt{3}$
B.2
C.3
D.6
B
).
A.$\sqrt{3}$
B.2
C.3
D.6
答案:
B [解析]
∵PA、PB 是⊙O 的切线,
∴PA=PB=1.
∵过点 C 的切线分别交 PA、PB 于点 D、E,
∴DA=DC,EC=EB.
∴△PDE 的周长=PD+PE+DE =PD+PE+DC+EC=PD+PE+DA+EB =PD+DA+PE+EB=PA+PB=2PA=2.故选 B.
∵PA、PB 是⊙O 的切线,
∴PA=PB=1.
∵过点 C 的切线分别交 PA、PB 于点 D、E,
∴DA=DC,EC=EB.
∴△PDE 的周长=PD+PE+DE =PD+PE+DC+EC=PD+PE+DA+EB =PD+DA+PE+EB=PA+PB=2PA=2.故选 B.
2. 如图,AB 为$\odot O$的直径,弦$CD\perp AB$于点 E,过点 C 作$\odot O$的切线交 AB 的延长线于点 M,下列结论:①$CE= DE$;②$\widehat{BC}= \widehat{BD}$;③MD 为$\odot O$的切线;④$MC= MD$. 其中正确的结论有(
A.1个
B.2个
C.3个
D.4个
D
).A.1个
B.2个
C.3个
D.4个
答案:
D [解析]
∵AB 为⊙O 的直径,弦 CD⊥AB,
∴CE=DE,故①正确;由 AB⊥CD,得$\overset{\frown}{BC}=\overset{\frown}{BD}$,故②正确;连接 OC、OD,则∠OCD=∠ODC.由 AB 垂直平分 CD,得 MC=MD,
∴∠MCD=∠MDC.又 MC 为⊙O 的切线,
∴MC⊥OC,
∴∠MCO=90°,即∠OCD+∠MCD=90°,
∴∠MDC+∠ODC=90°,即 OD⊥MD,
∴MD 为⊙O 的切线,故③④正确. 故选 D.
∵AB 为⊙O 的直径,弦 CD⊥AB,
∴CE=DE,故①正确;由 AB⊥CD,得$\overset{\frown}{BC}=\overset{\frown}{BD}$,故②正确;连接 OC、OD,则∠OCD=∠ODC.由 AB 垂直平分 CD,得 MC=MD,
∴∠MCD=∠MDC.又 MC 为⊙O 的切线,
∴MC⊥OC,
∴∠MCO=90°,即∠OCD+∠MCD=90°,
∴∠MDC+∠ODC=90°,即 OD⊥MD,
∴MD 为⊙O 的切线,故③④正确. 故选 D.
3. (2025·南京秦淮区期末)如图,射线 PA、PB 与$\odot O$相切,切点分别为 A、B,连接 PO 并延长,交$\odot O$于点 C,连接 AC、BC. 求证$AC= BC$.
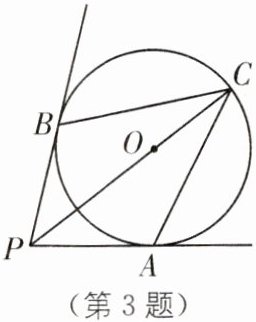

答案:
如图,连接 BO、AO.
∵射线 PA、PB 与⊙O 相切,切点分别为 A、B,
∴PA=PB,
∴点 P 在 AB 的垂直平分线上.
∵BO=AO,
∴点 O 在 AB 的垂直平分线上,
∴OP 垂直平分 AB.
∵点 C 在 PO 的延长线上,
∴AC=BC.一题多解 连接 BO、AO.
∵射线 PA、PB 与⊙O 相切,切点分别为 A、B,
∴PA=PB.
∵PA=PB,OA=OB,PO=PO,
∴△BPO≌△APO,
∴∠BOP=∠AOP.
∴180°-∠BOP=180°-∠AOP,即∠BOC=∠AOC,
∴AC=BC.
如图,连接 BO、AO.
∵射线 PA、PB 与⊙O 相切,切点分别为 A、B,
∴PA=PB,
∴点 P 在 AB 的垂直平分线上.
∵BO=AO,
∴点 O 在 AB 的垂直平分线上,
∴OP 垂直平分 AB.
∵点 C 在 PO 的延长线上,
∴AC=BC.一题多解 连接 BO、AO.
∵射线 PA、PB 与⊙O 相切,切点分别为 A、B,
∴PA=PB.
∵PA=PB,OA=OB,PO=PO,
∴△BPO≌△APO,
∴∠BOP=∠AOP.
∴180°-∠BOP=180°-∠AOP,即∠BOC=∠AOC,
∴AC=BC.

4. (2025·南通崇川区期中)如图,在$Rt\triangle ABC$中,$\angle C= 90^{\circ}$,$\odot O是\triangle ABC$的内切圆,三个切点分别为 D、E、F,若$BF= 4$,$AF= 6$,则$\triangle ABC$的面积是( ).
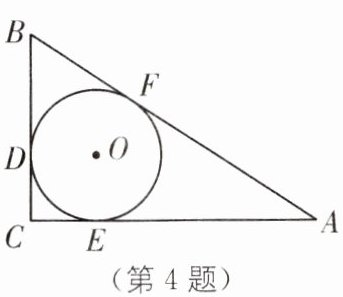
A.24
B.28
C.32
D.36

A.24
B.28
C.32
D.36
答案:
A [解析]如图,连接 DO、EO.
∵⊙O 是△ABC 的内切圆,切点分别为 D、E、F,
∴OE⊥AC,OD⊥BC,CD=CE,BD=BF=4,AF=AE=6,
∴AB=AF+BF=6+4=10.
∵∠C=90°,
∴四边形 OECD 是矩形.
∵EO=DO,
∴矩形 OECD 是正方形.设 EO=x,则 EC=CD=x,在 Rt△ABC 中,由勾股定理,得$BC^{2}+AC^{2}=AB^{2}$,故$(x+4)^{2}+(x+6)^{2}=10^{2}$,解得 x=2,
∴BC=6,AC=8,
∴$S_{\triangle ABC}=\frac{1}{2}×6×8=24$.故选 A.
A [解析]如图,连接 DO、EO.
∵⊙O 是△ABC 的内切圆,切点分别为 D、E、F,
∴OE⊥AC,OD⊥BC,CD=CE,BD=BF=4,AF=AE=6,
∴AB=AF+BF=6+4=10.
∵∠C=90°,
∴四边形 OECD 是矩形.
∵EO=DO,
∴矩形 OECD 是正方形.设 EO=x,则 EC=CD=x,在 Rt△ABC 中,由勾股定理,得$BC^{2}+AC^{2}=AB^{2}$,故$(x+4)^{2}+(x+6)^{2}=10^{2}$,解得 x=2,
∴BC=6,AC=8,
∴$S_{\triangle ABC}=\frac{1}{2}×6×8=24$.故选 A.

5. (2025·连云港海州区新港实验中学期中)如图,已知 PA、PB 是$\odot O$的两条切线,A、B 为切点,线段 OP 交$\odot O$于点 M. 给出下列四种说法:①$PA= PB$;②$OP\perp AB$;③四边形 OAPB 有外接圆;④M 是$\triangle ABP$的内心. 其中所有正确说法的个数是( ).

A.1
B.2
C.3
D.4

A.1
B.2
C.3
D.4
答案:
D [解析]
∵PA、PB 是⊙O 的两条切线,
∴PA=PB,∠OAP=∠OBP=90°,故①正确;
∵OA=OB,
∴△OAP≌△OBP(SSS),
∴△OAP、△OBP 关于 OP 对称,
∴OP⊥AB,故②正确;如图
(1),连接 AM、BM,则∠OAB+∠PAB=∠APM+∠PAB=90°,
∴∠OAB=∠APM.
∵OA=OM,
∴∠OAM=∠OMA,
∴∠OAB+∠BAM=∠APM+∠PAM,
∴∠BAM=∠PAM,即 AM 平分∠BAP,同理可得 BM 平分∠ABP,
∴M 是△ABP 的内心,故④正确;如图
(2),取 OP 的中点 Q,连接 AQ、BQ,则 AQ=$\frac{1}{2}$OP=BQ,即 QA=QO=QP=QB,
∴B、O、A、P 四点共圆,故③正确. 故选 D.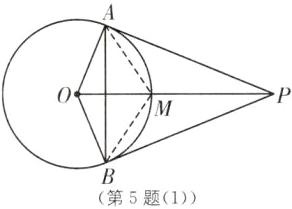

D [解析]
∵PA、PB 是⊙O 的两条切线,
∴PA=PB,∠OAP=∠OBP=90°,故①正确;
∵OA=OB,
∴△OAP≌△OBP(SSS),
∴△OAP、△OBP 关于 OP 对称,
∴OP⊥AB,故②正确;如图
(1),连接 AM、BM,则∠OAB+∠PAB=∠APM+∠PAB=90°,
∴∠OAB=∠APM.
∵OA=OM,
∴∠OAM=∠OMA,
∴∠OAB+∠BAM=∠APM+∠PAM,
∴∠BAM=∠PAM,即 AM 平分∠BAP,同理可得 BM 平分∠ABP,
∴M 是△ABP 的内心,故④正确;如图
(2),取 OP 的中点 Q,连接 AQ、BQ,则 AQ=$\frac{1}{2}$OP=BQ,即 QA=QO=QP=QB,
∴B、O、A、P 四点共圆,故③正确. 故选 D.


6. (2025·南京鼓楼区期中)如图,四边形 ABCD 是$\odot O$的外切四边形,且$BC= 3$,$AD= 5$,若四边形 ABCD 的面积等于 15,则$\odot O$的半径等于______.
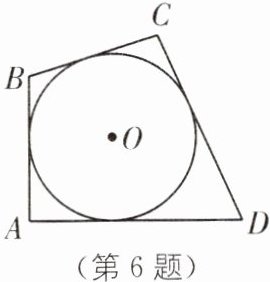

答案:
$\frac{15}{8}$ [解析]如图,连接 OA、OB、OC、OD,设四边形 ABCD 与⊙O 的切点分别为 E、F、G、H,连接 OE、OF,则 OE⊥AB,OF⊥AD.由切线长定理得 AE=AF,DF=DG,CG=CH,BE=BH,
∴AB+CD=BC+AD=8.设⊙O 的半径为 r,由题意,得$\frac{1}{2}AB\cdot r+\frac{1}{2}BC\cdot r+\frac{1}{2}AD\cdot r+\frac{1}{2}CD\cdot r=15$,解得$r=\frac{15}{8}$.
$\frac{15}{8}$ [解析]如图,连接 OA、OB、OC、OD,设四边形 ABCD 与⊙O 的切点分别为 E、F、G、H,连接 OE、OF,则 OE⊥AB,OF⊥AD.由切线长定理得 AE=AF,DF=DG,CG=CH,BE=BH,
∴AB+CD=BC+AD=8.设⊙O 的半径为 r,由题意,得$\frac{1}{2}AB\cdot r+\frac{1}{2}BC\cdot r+\frac{1}{2}AD\cdot r+\frac{1}{2}CD\cdot r=15$,解得$r=\frac{15}{8}$.

7. 分类讨论思想 如图,PA、PB 分别与$\odot O$相切于 A、B 两点,且$\angle APB= 56^{\circ}$,若点 C 是$\odot O$上异于点 A、B 的一点,则$\angle ACB$的大小为
62°或 118°
.
答案:
62°或 118° [解析]连接 CA、BC,
∵PA、PB 切⊙O 于点 A、B,
∴∠PAO=∠PBO=90°.
∵∠AOB+∠PAO+∠PBO+∠APB=360°,
∴∠AOB=360°-∠PAO-∠PBO-∠APB=360°-90°-90°-56°=124°.当点 C 在优弧 AB 上时,由圆周角定理知,∠ACB=$\frac{1}{2}$∠AOB=62°;当点 C 在劣弧 AB 上时,由圆内接四边形的性质,得∠ACB=118°.
∵PA、PB 切⊙O 于点 A、B,
∴∠PAO=∠PBO=90°.
∵∠AOB+∠PAO+∠PBO+∠APB=360°,
∴∠AOB=360°-∠PAO-∠PBO-∠APB=360°-90°-90°-56°=124°.当点 C 在优弧 AB 上时,由圆周角定理知,∠ACB=$\frac{1}{2}$∠AOB=62°;当点 C 在劣弧 AB 上时,由圆内接四边形的性质,得∠ACB=118°.
8. 如图,AB、AC 是$\odot O$的切线,B、C 是切点,过$\widehat{BC}$上的任意一点 P 作$\odot O$的切线与 AB、AC 分别交于点 D、E.
(1)连接 OD 和 OE,若$\angle A= 50^{\circ}$,则$\angle DOE= $
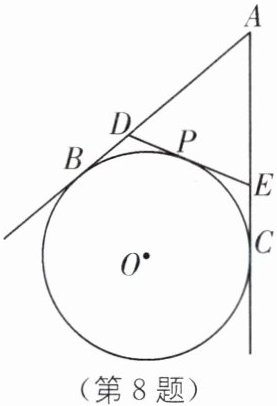
(2)当点 P 在$\widehat{BC}$的何处时,$PD= PE$?为什么?
当点 P 在$\overset{\frown}{BC}$的中点时,PD=PE. 理由如下:连接 OP、OB、OC,
∵P 为$\overset{\frown}{BC}$的中点,
∴∠POB=∠POC.
∵AB、AC、DE 为⊙O 的切线,
∴∠DOB=∠DOP,∠POE=∠COE,∠OBD=∠OCE=90°.
∴∠BOD=∠COE=∠POD=∠POE.
∴△BOD≌△COE.
∴OD=OE.又∠POD=∠POE,
∴PD=PE.
(1)连接 OD 和 OE,若$\angle A= 50^{\circ}$,则$\angle DOE= $
65
°.
(2)当点 P 在$\widehat{BC}$的何处时,$PD= PE$?为什么?
当点 P 在$\overset{\frown}{BC}$的中点时,PD=PE. 理由如下:连接 OP、OB、OC,
∵P 为$\overset{\frown}{BC}$的中点,
∴∠POB=∠POC.
∵AB、AC、DE 为⊙O 的切线,
∴∠DOB=∠DOP,∠POE=∠COE,∠OBD=∠OCE=90°.
∴∠BOD=∠COE=∠POD=∠POE.
∴△BOD≌△COE.
∴OD=OE.又∠POD=∠POE,
∴PD=PE.
答案:
(1)65
(2)当点 P 在$\overset{\frown}{BC}$的中点时,PD=PE. 理由如下:连接 OP、OB、OC,
∵P 为$\overset{\frown}{BC}$的中点,
∴∠POB=∠POC.
∵AB、AC、DE 为⊙O 的切线,
∴∠DOB=∠DOP,∠POE=∠COE,∠OBD=∠OCE=90°.
∴∠BOD=∠COE=∠POD=∠POE.
∴△BOD≌△COE.
∴OD=OE.又∠POD=∠POE,
∴PD=PE.
(1)65
(2)当点 P 在$\overset{\frown}{BC}$的中点时,PD=PE. 理由如下:连接 OP、OB、OC,
∵P 为$\overset{\frown}{BC}$的中点,
∴∠POB=∠POC.
∵AB、AC、DE 为⊙O 的切线,
∴∠DOB=∠DOP,∠POE=∠COE,∠OBD=∠OCE=90°.
∴∠BOD=∠COE=∠POD=∠POE.
∴△BOD≌△COE.
∴OD=OE.又∠POD=∠POE,
∴PD=PE.
查看更多完整答案,请扫码查看


