《2025年实验班提优训练九年级数学上册苏科版》

1.(2025·重庆八中期中)如图,在Rt△ABC中,∠A= 90°,AB= 4,AC= 3,分别以B、C为圆心,$\frac{1}{2}BC$长为半径画弧,交BC于点P,交AB于点M,交AC于点N,则图中阴影部分的面积为(A).

A.$6-\frac{25}{16}\pi$
B.$6-\frac{25}{8}\pi$
C.$12-\frac{25}{16}\pi$
D.$12-\frac{25}{8}\pi$

答案： A [解析]
∵∠A=90°,AB=4,AC=3,
∴∠B+∠C=90°,BC=√(AB²+AC²)=5.
∵以B、C为圆心,1/2BC长为半径画弧,
∴扇形CPN和扇形BPM的半径相同,均为5/2,
∴两个扇形的面积之和为((∠B+∠C)π×(5/2)²)/360°=25/16π,
∴阴影部分的面积为S_△ABC-25/16π=1/2×3×4-25/16π=6-25/16π.故选A.

2.(2025·天津河东区期末)如图,在扇形OAB中,已知∠AOB= 90°,OA= $\sqrt{2}$,过$\widehat{AB}$的中点C作CD⊥OA,CE⊥OB,垂足分别为D、E,则图中阴影部分的面积为______.

答案：
π/2-1 [解析]如图,连接OC,
∵CD⊥OA,CE⊥OB,
∴∠CDO=∠CEO=90°.
∵∠AOB=90°,
∴四边形CDOE是矩形.

∵点C是⌢AB的中点,
∴∠AOC=∠BOC.
在△COD与△COE中,
{∠CDO=∠CEO,
∠AOC=∠BOC,
OC=OC,
∴△COD≌△COE(AAS),
∴OD=OE.
∵四边形CDOE是矩形,
∴矩形CDOE是正方形.
∵OC=OA=√2,
∴2OE²=OC²=(√2)²=2,
∴OE=1,
∴图中阴影部分的面积=90π×(√2)²/360-1×1=π/2-1.

3.(2025·陕西西安临潼区期末)如图,在四边形ABCD中,已知∠A= 90°,分别以点B、C、D为圆心,以1 cm长为半径作圆,求阴影部分的面积之和.

答案：
∵⊙B、⊙C、⊙D的半径相同,
∴阴影部分面积之和等于三个扇形面积之和.
∵∠A=90°,
∴∠B+∠C+∠D=360°-90°=270°,
∴S_阴影部分面积之和=270π×1²/360=3/4π.

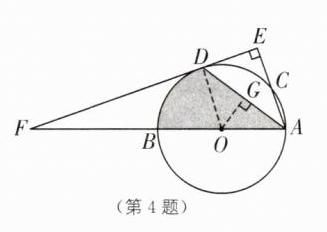
4.(2025·河北邢台任泽期中)如图,AB为⊙O的直径,AC是⊙O的一条弦,D为$\widehat{BC}$的中点,作DE⊥AC交AC的延长线于点E,交AB的延长线于点F,连接DA.
(1)若AB= 90 cm,则圆心O到EF的距离是多少?说明你的理由.
(2)若DA= DF= $6\sqrt{3}$,求阴影部分的面积(结果保留π).

答案：

(1)如图,连接OD.
∵D为⌢BC的中点,
∴∠CAD=∠BAD.
∵OA=OD,
∴∠BAD=∠ADO,
∴∠CAD=∠ADO,
∴OD//AE.
∵DE⊥AC,
∴OD⊥EF,
∴OD的长是圆心O到EF的距离.
∵AB=90cm,
∴OD=1/2AB=45cm.
(2)如图,过点O作OG⊥AD交AD于点G.
∵DA=DF,
∴∠F=∠BAD.
由
(1)得∠CAD=∠BAD,
∴∠F=∠CAD.
∵∠F+∠BAD+∠CAD=90°,
∴∠F=∠BAD=∠CAD=30°,
∴∠BOD=2∠BAD=60°,OF=2OD.
∵在Rt△ODF中,OF²-OD²=DF²,
∴(2OD)²-OD²=(6√3)²,解得OD=6,
在Rt△OAG中,OA=OD=6,∠OAG=30°,
∴OG=1/2×6=3,
∴S_△AOD=1/2×6√3×3=9√3,
∴S_阴影=S_扇形OBD+S_△AOD=60π×6²/360+9√3=6π+9√3.

5.(2025·天津滨海新区期末)如图,OA、OB为⊙O的半径,过点A作OA⊥AP,过点B作OB⊥BP,AP与BP相交于点P,连接OP交⊙O于点C,连接BC,若OA//BC,OA= 1.
(1)求证:△OBC为等边三角形;
(2)求图中阴影部分的面积(结果保留π).

答案：
(1)在Rt△OAP和Rt△OBP中,{OA=OB,
OP=OP,
∴Rt△OAP≌Rt△OBP(HL),
∴∠AOP=∠BOP.
∵OA//BC,
∴∠BCO=∠AOP,
∴∠BOP=∠BCO.
∵OB=OC,
∴∠OBC=∠BCO,
∴∠OBC=∠BCO=∠BOP,
∴△OBC为等边三角形;
(2)
∵△OBC为等边三角形,
∴∠BOP=60°,
∴∠OPB=30°,
∴OP=2OB=2OA=2,
∴BP=√(OP²-OB²)=√3,
∴S_Rt△OBP=S_Rt△OAP=1/2OB·BP=1/2×1×√3=√3/2.
∵∠AOB=2∠BOP=120°,
∴S_扇形AOB=120/360π×1²=π/3,
∴S_阴影=S_Rt△OBP+S_Rt△OAP-S_扇形AOB=√3-π/3.