《2025年实验班提优大考卷八年级物理上册苏科版》

16. (4分)在"比较纸锥下落快慢"实验中,首先取两张等大的圆形纸,分别剪成两个大小不等的扇形,再将它们做成两个锥角不等的纸锥.
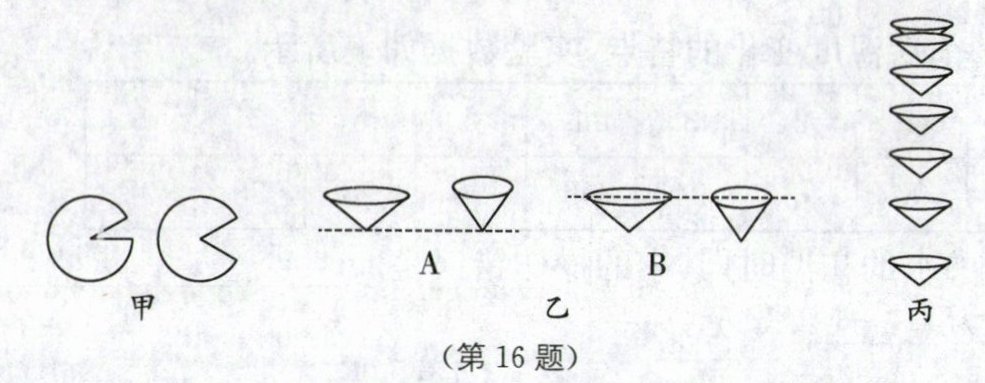
(1)为了比较纸锥下落的快慢,可将纸锥按如图乙中A(填"A"或"B")所示的位置释放,通过比较纸锥下落到地面时间来比较纸锥下落的快慢.
(2)为方便测量纸锥下落的时间,我们可采用锥角较大(填"大"或"小")的纸锥进行实验.小华用频闪照相机探究纸锥竖直下落的情况,由图丙可知,纸锥下落过程中做变速(填"匀速"或"变速")直线运动.

答案：
(1)A 时间
(2)大 变速 [解析]
(1)由控制变量思想可知，为了比较纸锥下落的快慢，应控制不同纸锥下落相同高度，通过比较纸锥下落到地面的时间比较快慢，故应从 A 位置释放纸锥.
(2)为方便测量纸锥下落的时间，可采用锥角较大的纸锥进行实验，控制纸锥下落速度；由图丙可知，纸锥相同时间内下落路程逐渐变大，故纸锥下落过程中做变速运动.

17. (5分)白蒲黄酒具有悠久的历史和独特的酿造工艺,被商务部认定为"中华老字号",如图所示为"12度2.5 L"精品白蒲纯净黄酒.

(1)将黄酒瓶密封后带到月球,酒的质量__________(填"变大""变小"或"不变").
(2)这瓶黄酒的密度为$1.02 g/cm^3,$则整瓶黄酒的质量为__________kg,倒出一半后,瓶中黄酒的密度__________(填"变大""变小"或"不变").
(3)酒的"度数"是指常温下酒精在酒中所占的体积百分比,则整瓶黄酒中所含酒精的质量为__________g.(ρ酒精$= 0.8 g/cm^3,$设水与酒精混合后总体积不变)
(4)若用此瓶装入相等体积的蜂蜜,总质量比原来增加了1 000 g,则所装蜂蜜的密度为$$_________$g/cm^3.$
(1)不变
(2)2.55不变
(3)240
(4)1.42

答案：
(1)不变
(2)2.55 不变
(3)240
(4)1.42[解析]
(1)将黄酒瓶密封后带到月球，酒的位置发生变化，酒的质量不变.
(2)黄酒的体积 $ V_{黄酒}=2.5\ L=2.5\ dm^3=2.5×10^3\ cm^3 $；整瓶黄酒的质量 $ m_{黄酒}=\rho_{黄酒}V_{黄酒}=1.02\ g/cm^3×2.5×10^3\ cm^3=2.55×10^3\ g=2.55\ kg $；倒出一半黄酒后，黄酒的物质种类、温度、状态不变，密度大小不变.
(3)一整瓶黄酒中酒精的体积 $ V_{酒精}=12\%×2.5×10^3\ cm^3=0.3×10^3\ cm^3 $；整瓶黄酒中酒精质量 $ m_{酒精}=\rho_{酒精}V_{酒精}=0.8\ g/cm^3×0.3×10^3\ cm^3=240\ g $.
(4)一瓶蜂蜜的质量 $ m_{蜂蜜}=m_{黄酒}+1000\ g=2.55\ kg+1\ kg=3.55\ kg=3.55×10^3\ g $，蜂蜜密度 $ \rho_{蜂蜜}=\frac{m_{蜂蜜}}{V_{黄酒}}=\frac{3.55×10^3\ g}{2.5×10^3\ cm^3}=1.42\ g/cm^3 $.

18. (6分)按题目要求作图.
(1)如图甲所示,作出三角形ABC通过平面镜所成的像.
(2)如图乙所示,一束光从空气斜射到玻璃表面,请用箭头在图中标出反射光线和折射光线的传播方向.
(3)如图丙所示,O为透镜光心,F为焦点,请完成光路.

答案：
18.
(1)如图所示 [解析]平面镜成像与成像物体关于平面镜对称.由三角形 ABC 三个顶点作关于平面镜对称点，用虚线连接 ABC 的像点 A'B'C'，即三角形 ABC 通过平面镜成的像.
(2)如图所示 [解析]光从空气斜射向玻璃表面，同时发生反射和折射现象.反射光线在空气中传播，方向沿远离入射点方向；折射光线进入玻璃中传播向远离入射点方向传播.
(3)如图所示 [解析]凸透镜对光线起会聚作用，由焦点发出的光线经凸透镜折射后，平行于主光轴；过光心的光线经凸透镜后，传播方向不变.归纳总结 凸透镜的三条特殊光线：①通过焦点的光线经凸透镜折射后将平行于主光轴.②平行于主光轴的光线经凸透镜折射后将过焦点.③过光心的光线经凸透镜折射后传播方向不改变.

19. (6分)新国标电动车标准要求电动自行车的最高车速不能超过25 km/h.张老师的家距离学校5 km,他每天骑着新国标电动车上下班.
(1)张老师骑着新国标电动车从家到达学校,最短需要多少时间?
(2)若张老师以5 m/s的速度在路上骑行30 s,此时间段内行驶了多长距离?
(3)若张老师从家到学校骑行用时1 000 s,中途又因红绿灯等因素多停留了250 s,则他在上班途中的平均速度为多少?

答案：
(1)0.2 h
(2)150 m
(3)4 m/s[解析]
(1)由 $ v=\frac{s}{t} $ 得，张老师骑着新国标电动车从家到达学校，最短需要时间 $ t_1=\frac{s_1}{v_1}=\frac{5\ km}{25\ km/h}=0.2\ h $.
(2)由 $ v=\frac{s}{t} $ 得，张老师 30 s 骑行距离 $ s_2=v_2t_2=5\ m/s×30\ s=150\ m $.
(3)总用时 $ t_3=1000\ s+250\ s=1250\ s $，平均速度 $ v_3=\frac{s}{t_3}=\frac{5000\ m}{1250\ s}=4\ m/s $.