《2025年实验班提优大考卷八年级物理上册苏科版》

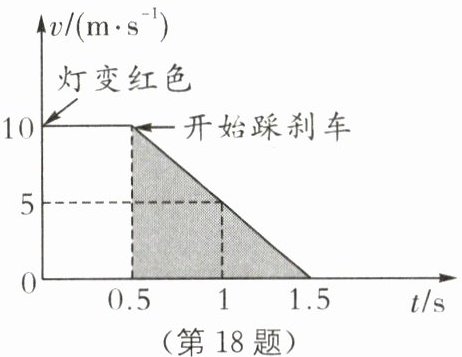
18.(2024·苏州昆山一模)汽车在公路上以10 m/s的速度匀速直线前进,司机发现前方路口信号灯变为红灯,经过0.5 s的反应时间后开始刹车,汽车速度v随时间t变化关系如图所示,则开始刹车后第0.5 s时,汽车速度为5m/s.从信号灯变红到汽车完全停止,这个过程中汽车的平均速度约为6.67m/s(精确到0.01).

答案： 18.5 6.67 [解析]由图像知,开始刹车后第0.5 s 时,汽车速度为5 m/s.由 v-t 图像中图线与时间轴围成的面积表示路程可知,从信号灯变红开始到汽车完全静止时车前进的距离$s_{总}=\frac{1}{2}×(0.5+1.5)×10\,m=10\,m$,从信号灯变红开始到车停下来为止,这段时间内车的平均速度$v'=\frac{s_{总}}{t_{总}}=\frac{10\,m}{1.5\,s}\approx 6.67\,m/s$.

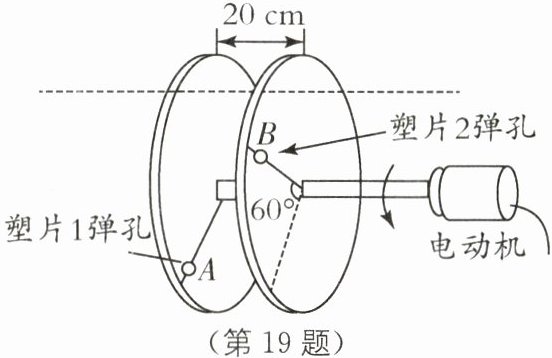
19.新情境 测子弹速度 (2024·苏州月考)在兵器工业中,子弹射出的速度是衡量枪械性能的指标之一.有一种运用旋转法测子弹速度的方法,如图所示,在电动机转轴上固定两个间距为20 cm的薄塑片,电动机以500 r/s匀速转动,枪械正对塑片水平射击,子弹穿越时受到的阻力不计.对一般步枪进行测试,子弹在两塑片之间飞行的这段时间内,塑片旋转不超过两圈.现对子弹速度在400 m/s以上的某型号步枪进行测试,子弹先后射穿两塑片的弹孔位置如图中的A、B.求:
(1)子弹在两塑片之间飞行的这段时间内,塑片转过的角度可能为__________.
(2)子弹在两塑片之间飞行的时间可能为__________s(结果用分数表示).
(3)该型号步枪子弹飞行的速度为__________m/s.

(1)60°
(2)$\frac{1}{3000}$
(3)600

答案： 19.
(1)$60^\circ$
(2)$\frac{1}{3000}$
(3)600 [解析]
(1)设子弹的速度取最小为400 m/s,子弹穿过两个塑片的时间$t=\frac{s}{v}=\frac{0.2\,m}{400\,m/s}=0.0005\,s$,电动机转过的圈数$n=500\,r/s×0.0005\,s=0.25\,r$,因为子弹速度取最低速度400 m/s 是0.25圈,实际速度是大于400 m/s,所以比0.25圈还少,所以转过角度小于$90^\circ$,所以可能转了$60^\circ$.
(2)电动机转过$60^\circ$的时间为$t'=\frac{1}{500}×\frac{60^\circ}{360^\circ}=\frac{1}{3000}\,s$,子弹在两塑片之间飞行的时间$t=t'=\frac{1}{3000}\,s$.
(3)由公式$v=\frac{s}{t}$得子弹飞行的速度$v'=\frac{s}{t}=\frac{0.2\,m}{\frac{1}{3000}\,s}=600\,m/s$.

20.(2024·苏州虎丘区模拟)汽车上的机械式里程表是用安装在车轮上的一组计数齿轮来实现计数的,它可以记录车轮转过的圈数.这些计数齿轮通过特定的传动装置被车轮的转动所驱动,同时车轮的转动还通过特定的传动装置传递给传感器,传感器将反映车轮转动情况的电信号显示在速度表上,从而指示此时的车速.当轮胎用久了有明显的磨损后,就会使所计里程和速度表上指示的时速产生误差.小明家汽车里程表记录的里程为30 000 km,则此汽车实际行驶的里程将小于(填"大于""等于"或"小于")该示数.若此车从苏州驶往上海,以速度表上指示的时速为依据,对整个行程所估算的时间将小于(填"大于""等于"或"小于")实际行驶时间.若已知小明家汽车新车轮的半径为350 mm,使用五年后,由于磨损,该轮胎的半径已比全新时减少了5 mm.这辆汽车从苏州开到上海的过程中,里程表示数增加了140 km,那么此过程中这辆车实际行驶的路程为138km.

答案： 20.小于 小于 138 [解析]如果轮胎有了磨损,轮半径减小,行驶相同的路程,车轮转动的圈数偏大,所以根据圈数测得的里程数和时速都要偏大,即实际行驶的里程将小于示数;因为从苏州到上海的路程是准确的,速度表上指示的时速偏大,所以,根据$t=\frac{s}{v}$估算的时间比实际用的时间要短;车轮直径为$r_0=350\,mm=0.35\,m$时,车轮转一圈走过的距离为车轮周长$L=2\pi r_0=2\pi×0.35\,m=0.7\pi\,m$,汽车里程表增加的数值为$s=140\,km=1.4×10^5\,m$,则车轮转过的圈数为$n=\frac{s}{L}=\frac{1.4×10^5\,m}{0.7\pi\,m/圈}=\frac{2×10^5}{\pi}\,圈$,轮胎的半径已比全新时减少了5 mm,半径为$r=0.345\,m$,此时车轮周长$L'=2\pi r=2\pi×0.345\,m=0.69\pi\,m$,因此这辆车实际行驶的路程为$s_{实}=nL'=\frac{2×10^5}{\pi}×0.69\pi\,m=1.38×10^5\,m=138\,km$.

21.(5分)化曲为直法 如图所示,这是一种测量曲线长度的方法,测量步骤如下:

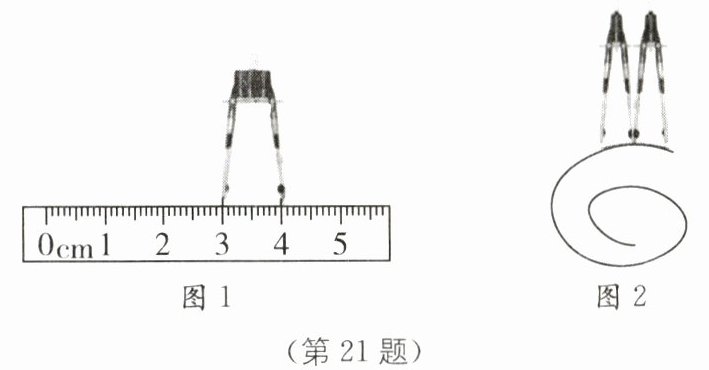
①将圆规两脚分开一小段距离,用刻度尺测出圆规两脚间距离,如图1所示;
②曲线可以看成是由许多段小线段组成的,记录用圆规量取小线段的数量,如图2所示.
(1)步骤①中刻度尺的分度值为1 mm,测得每段小线段的长度为1.00cm.
(2)步骤②中得到曲线的小线段数恰好为15段,则曲线长度为15.00cm.
(3)此方法测出的曲线长度比实际长度偏小(填"大"或"小").
(4)如果想减小误差,请你提出一个可行的方法:将圆规两脚间的距离调得更小一些.

答案： 21.
(1)1 mm 1.00
(2)15.00
(3)小
(4)将圆规两脚间的距离调得更小一些[解析]
(1)图1中,刻度尺上1 cm 之间有10个小格,所以一个小格代表的长度是0.1 cm=1 mm,即此刻度尺的分度值为1 mm;圆规左脚左侧与3.00 cm 对齐,右脚与4.00 cm 对齐,故小线段的长度为1.00 cm.
(2)步骤②中得到曲线的小线段数恰好为15段,则曲线长度为$L=1.00\,cm×15=15.00\,cm$.
(3)因为圆规两脚之间的距离小于两脚之间曲线的长度,所以测量结果偏小.
(4)将圆规两脚间的距离调得更小一些,这样用圆规去量取曲线小段时,就会更接近曲线的实际形状,能减小因用直线段近似替代曲线段而产生的误差.