《2025年暑假集训合肥工业大学出版社六年级数学人教版》

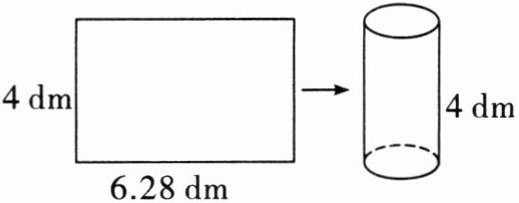
5. 李师傅家有一块长 $ 6.28 \mathrm{dm} $,宽 $ 4 \mathrm{dm} $ 的白铁皮,他想做一个高 $ 4 \mathrm{dm} $ 的容积最大的圆柱形无盖水桶(接口处材料不考虑)。于是,他到店里去配一个底,可是商店里没有圆形的白铁皮,只能根据需要先剪下一块长方形或正方形的白铁皮,再裁成圆形。
(1)你认为李师傅该剪下怎样的一块长方形或正方形白铁皮？写出你的理由。
(2)算一算,做成的水桶一次最多可盛水多少千克？($ 1 \mathrm{dm}^{3} $ 水重 $ 1 \mathrm{kg} $)

答案：
(1) 两种情况：
若以$6.28\mathrm{dm}$作为圆柱底面的周长，则底面半径$r_1$为：
$r_1=\frac{6.28}{2\pi}=\frac{6.28}{2 × 3.14}= 1 \mathrm{dm}$，
那么需剪下边长为$2 \mathrm{dm}$的正方形白铁皮，再裁成圆形。
若以$4\mathrm{dm}$作为圆柱底面的周长，则底面半径$r_2$为：
$r_2=\frac{4}{2\pi}=\frac{4}{2 × 3.14}\approx 0.64 \mathrm{dm}$，
那么需剪下边长至少为$4\mathrm{dm}$的长方形白铁皮，再裁成圆形。
因为$2\gt0.64$，
所以，为了制作一个容积最大的圆柱形无盖水桶，李师傅应该选择剪下边长为$2\mathrm{dm}$的正方形白铁皮，再裁成圆形。
(2) 底面半径$r = 1 \mathrm{dm}$，高$h = 4 \mathrm{dm}$，
那么水桶的容积$V$为：
$V=\pi r^2h=3.14 × 1^2 × 4=12.56 \mathrm{dm}^3$，
由于$1\mathrm{dm}^3$水重$1\mathrm{kg}$，
所以水桶一次最多可盛水：
$12.56 × 1=12.56 \mathrm{kg}$。
因此，做成的水桶一次最多可盛水$12.56\mathrm{kg}$。

6. 有一个圆柱,它的底面周长与高相等。如果高缩短 $ 2 \mathrm{cm} $,表面积就减少 $ 6.28 \mathrm{cm}^{2} $,求这个圆柱的体积。

答案： 底面周长：$6.28÷2 = 3.14(\text{cm})$
底面半径：$3.14÷3.14÷2 = 0.5(\text{cm})$
圆柱的高：$3.14\text{cm}$
圆柱体积：$3.14×0.5^{2}×3.14 = 3.14×0.25×3.14 = 0.785×3.14 = 2.4649(\text{cm}^{3})$
答：这个圆柱的体积是$2.4649\,\text{cm}^3$。

7. 一个圆锥形的麦堆,底面半径为 $ 2 \mathrm{m} $,高 $ 1.5 \mathrm{m} $,如果把这些小麦装入一个圆柱形粮囤里,只占粮囤容积的 $ \frac{4}{9} $。已知粮囤底面积是 $ 9 \mathrm{m}^{2} $,粮囤的高是多少米？

答案： 解析：
题目考查圆锥和圆柱的体积计算。
首先，根据圆锥体积公式 $V = \frac{1}{3} \pi r^2 h$，其中 $r$ 是底面半径，$h$ 是高，
代入数值 $r = 2\text{m}$ 和 $h = 1.5\text{m}$ 得到圆锥体积为：
$V_{\text{圆锥}} = \frac{1}{3} \pi × 2^2 × 1.5 = \frac{1}{3} \pi × 4 × 1.5 = 2\pi \text{m}^3$，
接着，设圆柱粮囤的高为 $H$ 米，其底面积为 $9\text{m}^2$，
根据圆柱体积公式 $V = S H$，其中 $S$ 是底面积，
因为圆锥形麦堆的小麦只占粮囤容积的 $\frac{4}{9}$，所以有：
$2\pi = \frac{4}{9} × 9H$，
化简得：
$2\pi = 4H$，
解得 $H = \frac{1}{2}\pi \approx 1.57$（取 $\pi \approx 3.14$），
答案：
粮囤的高约为$1.57$米。

8. 如下图,一个底面直径为 $ 20 \mathrm{cm} $ 的装有一部分水的圆柱形容器,水中放着一个底面直径 $ 12 \mathrm{cm} $,高 $ 10 \mathrm{cm} $ 的圆锥形铅锤,铅锤全部浸入水中。当铅锤从水中取出后,容器中水面高度下降了几厘米？

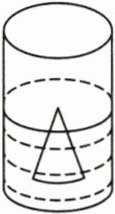
答案： 解析：本题主要考查圆柱和圆锥的体积计算，以及利用体积变化求水面高度下降的值。需要先分别求出圆锥的体积，再根据圆锥体积等于水面下降部分水的体积，结合圆柱底面积公式求出水面下降的高度。
1. 计算圆锥的体积：
圆锥体积公式为$V_{锥}=\frac{1}{3}\pi r^{2}h$（其中$r$是底面半径，$h$是高）。
已知圆锥底面直径为$12cm$，则半径$r = 12÷2 = 6cm$，高$h = 10cm$。
将$r = 6$、$h = 10$代入圆锥体积公式可得：
$V_{锥}=\frac{1}{3}×\pi×6^{2}×10=\frac{1}{3}×\pi×36×10 = 120\pi(cm^{3})$。
2. 计算圆柱形容器的底面积：
圆柱底面积公式为$S_{柱底}=\pi R^{2}$（其中$R$是底面半径）。
已知圆柱底面直径为$20cm$，则半径$R = 20÷2 = 10cm$。
将$R = 10$代入圆柱底面积公式可得：
$S_{柱底}=\pi×10^{2}=100\pi(cm^{2})$。
3. 计算水面下降的高度：
因为圆锥从水中取出后，水面下降部分水的体积等于圆锥的体积，设水面下降的高度为$h_{降}$。
根据圆柱体积公式$V = S_{柱底}h_{降}$，可得$h_{降}=\frac{V_{锥}}{S_{柱底}}$。
将$V_{锥}=120\pi$、$S_{柱底}=100\pi$代入上式可得：
$h_{降}=\frac{120\pi}{100\pi}=1.2(cm)$。
答案：$1.2cm$。

9. 李大爷将一些玉米堆放在室内的一个墙角(如图墙面与墙面,墙面与地面均垂直)。玉米堆的形状近似 $ \frac{1}{4} $ 个圆锥。测得地面上 $ A $ 点和 $ B $ 点到墙角的距离均为 $ 1 \mathrm{m} $,且这堆玉米的高为 $ 1.2 \mathrm{m} $。已知每立方米玉米约重 $ 750 \mathrm{kg} $,这堆玉米的质量约为多少千克？

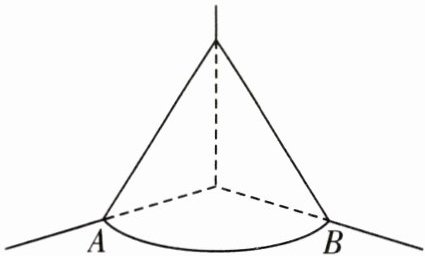
答案： 解析：本题可先根据圆锥体积公式求出$\frac{1}{4}$圆锥的体积，再结合每立方米玉米的重量求出这堆玉米的质量。
1. 计算玉米堆（$\frac{1}{4}$圆锥）的底面半径：
已知地面上$A$点和$B$点到墙角的距离均为$1m$，即圆锥底面半径$r = 1m$。
2. 计算玉米堆（$\frac{1}{4}$圆锥）的体积：
圆锥体积公式为$V=\frac{1}{3}\pi r^{2}h$（其中$V$是圆锥体积，$r$是底面半径，$h$是高）。
那么$\frac{1}{4}$圆锥的体积$V_{玉米堆}=\frac{1}{4}×\frac{1}{3}\pi r^{2}h$，将$r = 1m$，$h = 1.2m$代入可得：
$V_{玉米堆}=\frac{1}{4}×\frac{1}{3}×3.14×1^{2}×1.2$
$=\frac{1}{4}×\frac{1}{3}×3.14×1×1.2$
$=\frac{1}{4}×0.4×3.14$
$= 0.1×3.14$
$= 0.314$（立方米）
3. 计算这堆玉米的质量：
已知每立方米玉米约重$750kg$，根据质量 = 体积×每立方米重量，可得这堆玉米的质量为：
$0.314×750 = 235.5$（千克）
答案：
这堆玉米的质量约为$235.5$千克。