《2025年暑假集训合肥工业大学出版社六年级数学人教版》

例2 两个三角形拼成如下图左边的图形,怎样变换才能得到右边的图形?


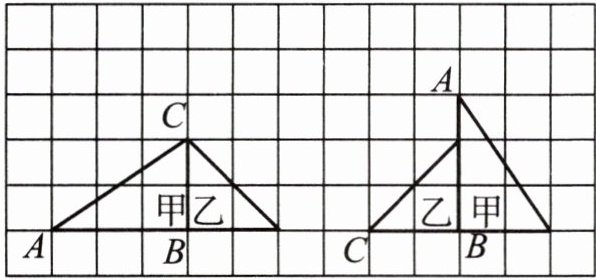
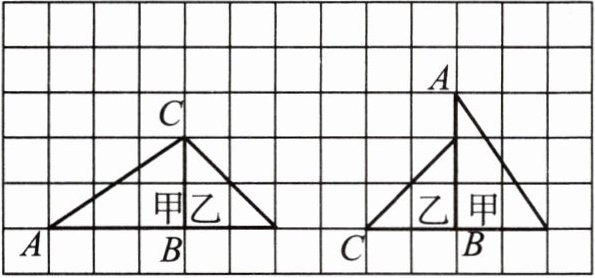
【解析】变换的方法有很多种,只需写出一种即可。
【答案】例如:先将左图整体向右平移6格,再将甲三角形绕B点顺时针旋转90°,接着再将乙三角形绕B点逆时针旋转90°,就可以得到右图。

答案： 解析：本题考查图形的平移和旋转。通过平移和旋转的方式，将左图变换为右图。
答案：先将左图整体向右平移6格，再将甲三角形绕B点顺时针旋转$90^\circ$，接着再将乙三角形绕B点逆时针旋转$90^\circ$，就可以得到右图。

例3 将一个圆按2:1的比放大时,下面( )种方法是错误的。

A.将半径按2:1的比放大
B.将周长按2:1的比放大
C.将面积按2:1的比放大
【解析】本题考查了图形的放大与缩小的基本特征,将图形按2:1放大,只是将半径或周长按2:1放大,而将面积按4:1的比放大,形状始终不变。
【答案】C

答案： 【解析】本题考查图形放大与缩小的性质。
当一个圆按2:1的比例放大时，其所有线性尺寸（如半径、直径、周长）都会按照2:1的比例放大。
但是，面积是二维的，所以当线性尺寸放大2倍时，面积会放大$2^2=4$倍。
A选项：将半径按2:1的比放大，这是正确的，因为圆的半径是线性尺寸。
B选项：将周长按2:1的比放大，这也是正确的，因为周长也是圆的线性尺寸，周长与半径成正比，半径放大2倍，周长也会放大2倍。
C选项：将面积按2:1的比放大，这是错误的。因为当圆的半径放大2倍时，面积会放大4倍，而不是2倍。
【答案】C

例4 如图是月湖公园的示意图,据图回答问题。

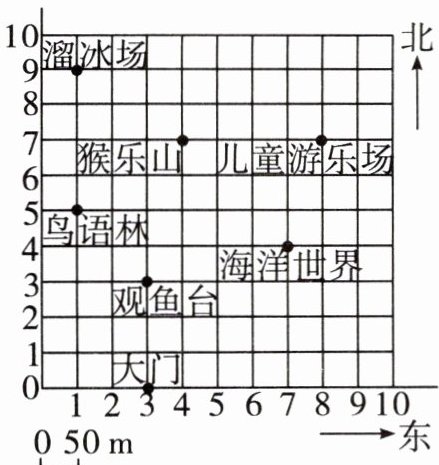
(1)公园的大门位于( , ),向北走150m,到达( )。
(2)儿童游乐场位于( , ),在大门的( )偏( )约( )m处。
(3)溜冰场位于( , ),在大门的( )偏( )约( )m处。
(4)溜冰场向南走200m,到达鸟语林;猴乐山与这两处的距离相等,距儿童游乐场200m,位于( , )。
(5)海洋世界在大门北偏东约280m,位于( , )。
【解析】此题属于图形与位置的综合练习,要求在有刻度的方格纸上,用数对表示位置,由数对确定点,由点写出数对;由方向和距离确定点,由点的对应位置写出方向和距离。
【答案】(1)(3,0) 观鱼台 (2)(8,7) 北 东 430 (3)(1,9) 北 西 460 (4)(4,7) (5)(7,4)

答案： 解析：
本题主要考查用数对表示位置以及根据方向和距离确定点的位置。
在数对中，第一个数表示列，第二个数表示行。
根据图中所给信息，结合方向（上北下南，左西右东）和距离（一小格代表$50m$）来确定各点的位置。
大门位于$(3,0)$，向北走$150m$，即向上走$150÷50 = 3$格，到达$(3,3)$，也就是观鱼台。
儿童游乐场位于$(8,7)$，大门位置是$(3,0)$，从大门到儿童游乐场，水平方向向右走了$8 - 3 = 5$格，距离是$5×50 = 250m$，垂直方向向上走了$7 - 0 = 7$格，距离是$7×50 = 350m$，根据勾股定理可得距离约为$\sqrt{250^{2}+350^{2}}\approx430m$，方向是北偏东。
溜冰场位于$(1,9)$，大门位置是$(3,0)$，从大门到溜冰场，水平方向向左走了$3 - 1 = 2$格，距离是$2×50 = 100m$，垂直方向向上走了$9 - 0 = 9$格，距离是$9×50 = 450m$，根据勾股定理可得距离约为$\sqrt{100^{2}+450^{2}}\approx460m$，方向是北偏西。
溜冰场$(1,9)$向南走$200m$，即向下走$200÷50 = 4$格，到达$(1,5)$。猴乐山与溜冰场、鸟语林的距离相等，距儿童游乐场$200m$，即$200÷50 = 4$格，所以猴乐山位于$(4,7)$。
海洋世界在大门北偏东约$280m$，$280÷50 = 5.6$格，根据方向和距离可确定其位于$(7,4)$。
答案：
(1)$(3,0)$；观鱼台
(2)$(8,7)$；北；东；$430$
(3)$(1,9)$；北；西；$460$
(4)$(4,7)$
(5)$(7,4)$

例5 某地区发生的大地震震中位于该市市中心以东130km处,地震震中南偏西70°,距震中180km处就是核电站。如何根据该市市中心的位置确定地震震中位置和核电站的位置?画出平面图。
【解析】首先要根据答题位置确定合适的比例尺1:4000000,根据比例尺分别计算出该市市中心距震中、震中距核电站的图上距离。根据求出的图上距离画出该市市中心以东3.25cm处的震中位置,由震中位置出发,南偏西70°4.5cm的位置为核电站。
【答案】比例尺1:4000000 130km= 13000000cm 13000000×$\frac{1}{4000000}$= 3.25(cm) 180km= 18000000cm 18000000×$\frac{1}{4000000}$= 4.5(cm)

答案： 【解析】
本题主要考查了位置与方向及比例尺的应用。
需要根据题目给出的实际距离和角度，利用比例尺计算出图上的距离，然后依据方向画出震中和核电站的位置。
首先，确定一个合适的比例尺，这里选择$1:4000000$，意味着图上$1cm$代表实际的$4000000cm$，根据$1km=100000cm$，所以$4000000cm=40km$。
然后，根据比例尺分别计算出该市市中心距震中、震中距核电站的图上距离。
该市市中心距震中的实际距离是$130km$，转换为厘米是$13000000cm$，利用比例尺计算出图上的距离：
$13000000 × \frac{1}{4000000} = 3.25(cm)$。
震中距核电站的实际距离是$180km$，转换为厘米是$18000000cm$，利用比例尺计算出图上的距离：
$18000000 × \frac{1}{4000000} = 4.5(cm)$。
最后，根据计算出的图上距离和题目给出的方向，可以在图上画出震中和核电站的位置。
先画出该市市中心以东$3.25cm$处的震中位置，再由震中位置出发，南偏西$70^\circ$画$4.5cm$的位置为核电站。
【答案】
比例尺$1:4000000$；
$130km = 13000000cm$；
$13000000 × \frac{1}{4000000} = 3.25(cm)$；
$180km = 18000000cm$；
$18000000 × \frac{1}{4000000} = 4.5(cm)$；
图略（根据描述，在图上画出该市市中心以东$3.25cm$处为震中，再由震中出发南偏西$70^\circ$画$4.5cm$为核电站）。