《2025年暑假集训合肥工业大学出版社六年级数学人教版》

例1 下面是一个立体图形的展开图。(单位:cm)

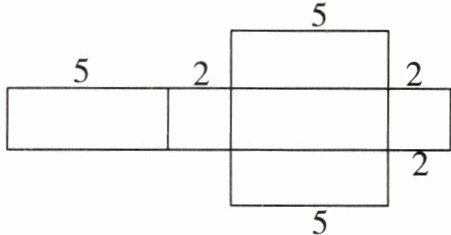
(1)这个展开图可以折成( )体。
(2)折成的立体图形棱长是5cm的有( )条。棱长的总和是( )。
【解析】 观察图,这是一个有两个面为正方形的长方体,正方形的边长为2cm,棱长为5cm的有4条,棱长总和为$2×8 + 5×4 = 36(cm)$。
【答案】 (1)长方 (2)4 36cm

答案：
(1)观察展开图可知，它有两个相对的面是正方形，其余四个面是长方形，且相对的面相等，所以这个展开图可以折成长方体。
本题答案为：长方。
(2)折成的长方体中，棱长是$5cm$的有$4$条（长方体的四条高）。
棱长总和为：
$(5+2+2)× 4=36(cm)$。
本题答案为：4；$36cm$。

例2 选一选。下面三个图形中,不能折成正方体的图形是( )。

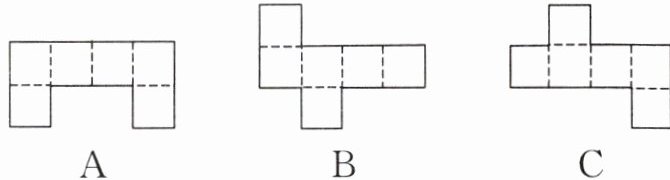
【解析】 在这里我们可以根据正方体的11种展开图来判断,A图只有两行,而正方体展开图的11种形状中只有两行的是“33”型,因此A图不能折成正方体,而B图、C图恰好都是“141”型,可以折成正方体。
【答案】 A

答案： 解析：本题可根据正方体展开图的特征来判断各选项能否折成正方体。正方体展开图有“1 - 4 - 1”型、“2 - 3 - 1”型、“2 - 2 - 2”型、“3 - 3”型等多种类型。
选项A：该图形只有两行，正方体展开图中只有两行的是“3 - 3”型，但此图形不符合“3 - 3”型的特征，所以不能折成正方体。
选项B：该图形属于“1 - 4 - 1”型，符合正方体展开图的特征，可以折成正方体。
选项C：该图形同样属于“1 - 4 - 1”型，符合正方体展开图的特征，可以折成正方体。
答案：A。

例3 下面这些物体哪些是圆柱,哪些是圆锥?

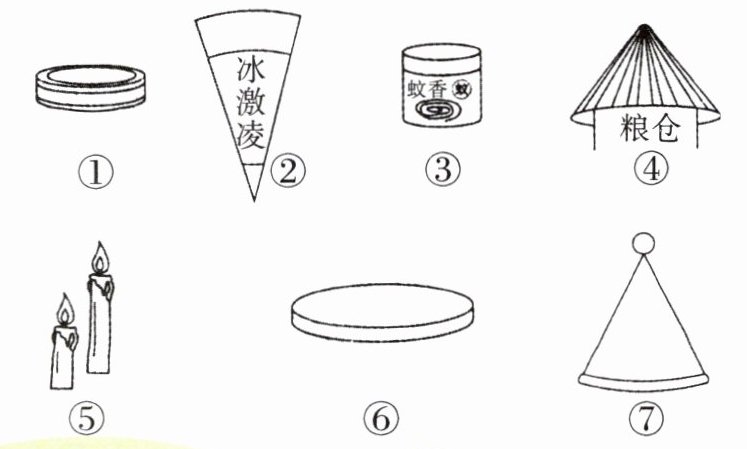
【解析】 由圆柱、圆锥定义可判断①③⑥⑤是圆柱,②④⑦是圆锥。
【答案】 ①③⑥⑤是圆柱;②④⑦是圆锥。

答案： ①③⑤⑥是圆柱；②④⑦是圆锥。

例4 一个游泳池的长是80m,宽是60m,深是2.5m,在它的四壁和底部涂抹水泥,如果每平方米需要水泥6kg,一共需要多少千克水泥?这个游泳池最多可容水多少立方米?
【解析】 由题意可知,游泳池的四壁和底部涂水泥,实际是涂五个面,先求出这五个面的面积和,再根据每平方米需要水泥6kg,求出一共需要水泥多少千克。求游泳池最多容水多少立方米,就是求这个游泳池的容积是多少。
【答案】 $6×[(80×2.5 + 60×2.5)×2 + 80×60]= 33000(kg)$$80×60×2.5 = 12000(m^{3})$

答案： 【解析】
题目考查长方体表面积和体积的计算。
涂抹水泥的部分是游泳池的四壁和底部，共五个面。
先求这五个面的面积和，再乘以每平方米所需的水泥质量，得到总水泥质量。
求游泳池最多可容水多少立方米，即求游泳池的容积，用长×宽×深计算。
【答案】
涂抹水泥的面积：
$(80× 2.5+60× 2.5)× 2+80× 60$
$=(200+150)× 2+4800$
$=350× 2+4800$
$=700+4800$
$=5500(m^{2})$
所需水泥质量：
$6× 5500=33000(kg)$
游泳池的容积：
$80× 60× 2.5=12000(m^{3})$
答：一共需要$33000$千克水泥，这个游泳池最多可容水$12000$立方米。

例5 把一根长1m,底面直径是2dm的圆柱形钢材截成4段,表面积增加了多少?
【解析】 把钢材截成4段,是将圆柱平行于底面截$(4 - 1)$次,而每次都要增加两个底面的面积。
【答案】 $3.14×(2÷2)^{2}×[(4 - 1)×2]= 3.14×6 = 18.84(dm^{2})$

答案： 把钢材截成4段，需截$4 - 1 = 3$次，每次增加2个底面面积，共增加$3×2 = 6$个底面面积。
底面半径为$2÷2 = 1(dm)$，底面积为$3.14×1^{2} = 3.14(dm^{2})$。
表面积增加了$3.14×6 = 18.84(dm^{2})$。
答：表面积增加了$18.84dm^{2}$。

例6 把直角三角形ABC沿BC边和AB边分别旋转一周,得到两个圆锥(如下图),哪个圆锥的体积大?

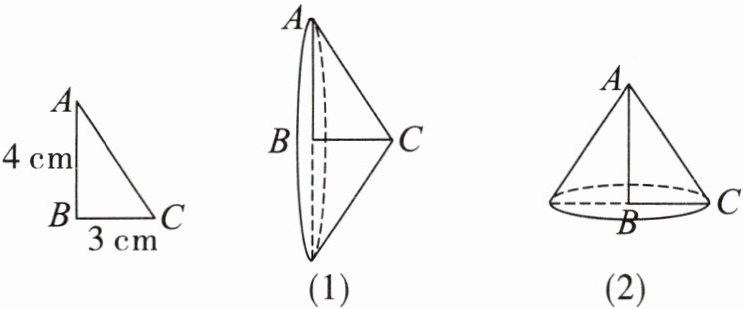
【解析】 把直角三角形旋转一周形成圆锥,以哪条直角边为轴旋转,这条直角边就是圆锥的高,另一条直角边就是圆锥的底面半径。
【答案】 图(1)中,圆锥的底面半径是4cm,高是3cm,则体积是$3.14×4^{2}×3×\frac{1}{3}= 3.14×16×3×\frac{1}{3}= 50.24(cm^{3})$;图(2)中,圆锥的底面半径是3cm,高是4cm,则体积是$3.14×3^{2}×4×\frac{1}{3}= 3.14×9×4×\frac{1}{3}= 37.38(cm^{3})$,$50.24＞37.68$,圆锥(1)的体积大。

答案： 解析：本题主要考查圆锥的体积计算。
以直角三角形的直角边为轴旋转一周所形成的图形是圆锥，为轴的直角边就是圆锥的高，另一条直角边就是圆锥的底面半径。
根据圆锥的体积公式$V=\frac{1}{3}\pi r^{2}h$（其中$r$是底面半径，$h$是高）分别计算两个圆锥的体积，再比较大小。
答案：
图
(1)中，圆锥的底面半径是$4cm$，高是$3cm$，
则体积是：
$3.14×4^{2}×3×\frac{1}{3}$
$=3.14×16×3×\frac{1}{3}$
$=50.24(cm^{3})$
图
(2)中，圆锥的底面半径是$3cm$，高是$4cm$，
则体积是：
$3.14×3^{2}×4×\frac{1}{3}$
$=3.14×9×4×\frac{1}{3}$
$=37.68(cm^{3})$
因为$50.24＞37.68$，
所以圆锥
(1)的体积大。