《2025年暑假集训合肥工业大学出版社六年级数学人教版》

例2 两人骑摩托车同时出发,几小时后相遇？

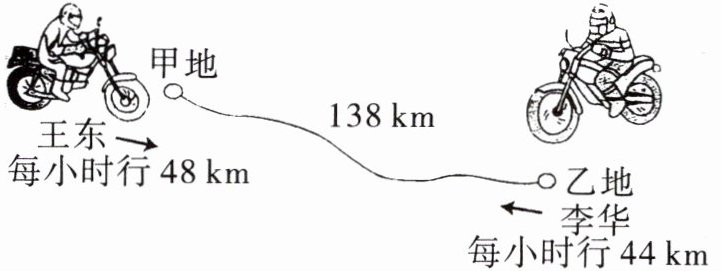
【解析】 此题主要是对列方程解决问题等知识的考查。先找出题中的未知量(即所求问题),设为x；再找出题中的等量关系。题中的等量关系式是：(王东的速度+李华的速度)×相遇时间= 总路程,根据等量关系式列出方程。
【答案】 解：设x小时后相遇。
$(48+44)x= 138$ $48x+44x= 138$
$92x= 138$ $92x= 138$
$92x÷92= 138÷92$ 或 $92x÷92= 138÷92$
$x= 1.5$ $x= 1.5$
答：1.5小时后相遇。

答案： 解析：本题主要考查列方程解决相遇问题。需要找出题目中的等量关系，即两人的速度和乘以相遇时间等于总路程，然后通过设未知数列出方程并求解。
答案：解：设$x$小时后相遇。
$(48 + 44)x = 138$
$92x = 138$
$92x÷92 = 138÷92$
$x = 1.5$
答：$1.5$小时后相遇。

例3 填空。
(1) 一项工程,甲单独做要4天完成,乙单独做要5天完成,甲和乙的工作效率比是( )。
(2) 把$2m:4cm$化成最简单的整数比是( ),比值是( )。
【解析】 (1) 要求甲、乙的工作效率比,关键是要先根据工作总量和工作时间求出甲、乙的工作效率,再相比,即$\frac{1}{4}:\frac{1}{5}= 5:4$；(2) 为了简便,化简比和求比值时可以都用前项除以后项,但要注意结果的区别。由于单位不统一,在化简前要先统一单位,即$2m:4cm= 200cm:4cm= 50:1= 50$。
【答案】 (1)$5:4$ (2)$50:1$ 50

答案： 【解析】
(1) 要求甲、乙的工作效率比，我们需要先根据工作总量（设为1）和各自的工作时间求出甲、乙的工作效率。甲单独做要4天完成，所以甲的工作效率是$\frac{1}{4}$；乙单独做要5天完成，所以乙的工作效率是$\frac{1}{5}$。然后，我们比较这两个效率，即$\frac{1}{4}:\frac{1}{5}$，通过交叉相乘得到$5:4$。
(2) 要把$2m:4cm$化成最简单的整数比，我们首先要统一单位。由于$1m=100cm$，所以$2m=200cm$。然后，我们比较$200cm$和$4cm$，得到$200:4$，简化后得到$50:1$。比值是前项除以后项的结果，即$50 ÷ 1 = 50$。
【答案】
(1) $5:4$
(2) $50:1$，比值是$50$

例4 小兰把3根1米长的绳子平均分给了5个人做手工,每人分得多少米？
【解析】 这是一道平均分的实际问题,这里3米是总数量,5个人是总份数,求的是每份数,根据除法的意义可列式为$3÷5$,我们可以发现分得的结果不满1,也就是我们常说的不够除,这时我们可以用分数来表示$3÷5$的结果。我们可以把3根绳子摞在一起,平均分成5份,剪开,每人分得3米的$\frac{1}{5}$,也就是$\frac{3}{5}$米,即$3÷5= \frac{3}{5}$(米),如图所示。

我们仔细观察$3÷5= \frac{3}{5}$这个算式,会发现两个数相除如果得不到整数商,可以用分数表示,除法算式中被除数相当于分数的分子,除数相当于分数的分母,除号相当于分数的分数线。
【答案】$3÷5= \frac{3}{5}$(米)
答：每人分得$\frac{3}{5}$米。

答案： 答案略

例5 印刷厂装订一批书,每天装订3.5万册,需要12天完成。如果每天装订3万册,多少天可以完成？
【解析】 本题考查比例知识的应用。应该先判断这道题是成正比例还是反比例,再解答。因为每天装订册数×装订天数= 装订总数,所以每天装订册数和装订天数成反比例。
【答案】 解：设x天可以完成。
$3x= 3.5×12$
$x= 3.5×12÷3$
$x= 14$
答：14天可以完成。

答案： 【解析】本题考查比例知识的应用。
题目描述了印刷厂装订书的情况，给出了两种装订速度下所需的天数，并询问如果改变装订速度，需要多少天完成。
因为每天装订册数×装订天数=装订总数，所以每天装订册数和装订天数成反比例。
我们可以利用反比例关系建立方程来求解。
【答案】 解：设$x$天可以完成。
根据反比例关系，我们有：
$3x = 3.5 × 12$
$x = \frac{3.5 × 12}{3}$
$x = 14$
答：$14$天可以完成。