2025年暑假集训合肥工业大学出版社六年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假集训合肥工业大学出版社六年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
5. 把一个平行四边形拉成一个长方形,它的周长( ),面积( )。
A.变大
B.不变
C.变小
A.变大
B.不变
C.变小
答案:
解析:本题可根据平行四边形和长方形的周长及面积的计算方法,结合平行四边形拉成长方形的过程中边长和高度的变化情况来进行分析。
周长变化情况:
将平行四边形拉成长方形的过程中,四条边的长度并没有发生改变。因为周长是围成图形的所有边长的总和,所以它的周长不变,应选B。
面积变化情况:
平行四边形的面积公式为$S = 底×高$,当把平行四边形拉成长方形时,底的长度不变,但是高变长了(平行四边形的高小于斜边,拉成长方形后高与斜边重合,高变长)。根据面积公式,底不变,高变大,那么面积就会变大,所以它的面积变大,应选A。
答案:B;A
周长变化情况:
将平行四边形拉成长方形的过程中,四条边的长度并没有发生改变。因为周长是围成图形的所有边长的总和,所以它的周长不变,应选B。
面积变化情况:
平行四边形的面积公式为$S = 底×高$,当把平行四边形拉成长方形时,底的长度不变,但是高变长了(平行四边形的高小于斜边,拉成长方形后高与斜边重合,高变长)。根据面积公式,底不变,高变大,那么面积就会变大,所以它的面积变大,应选A。
答案:B;A
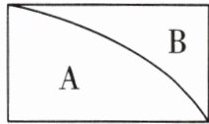
6. 如右图,图形A的周长( )图形B的周长,图形A的面积( )图形B的面积。
A.等于
B.大于
C.小于

A.等于
B.大于
C.小于
答案:
解析:本题考查图形的周长和面积的比较。需要根据图形特点,分别分析两个图形的周长和面积。
图形A和图形B的周长:
图形A的周长由长方形的长、宽以及弧形部分组成。
图形B的周长由长方形的长、宽以及弧形部分组成。
由于两个图形共用长方形的长和宽,且弧形部分是同一个四分之一圆弧,所以它们的周长相等。
图形A和图形B的面积:
图形A的面积等于长方形的面积减去四分之一圆的面积。
图形B的面积等于四分之一圆的面积。
显然,图形A的面积大于图形B的面积。
答案:A;B。
图形A和图形B的周长:
图形A的周长由长方形的长、宽以及弧形部分组成。
图形B的周长由长方形的长、宽以及弧形部分组成。
由于两个图形共用长方形的长和宽,且弧形部分是同一个四分之一圆弧,所以它们的周长相等。
图形A和图形B的面积:
图形A的面积等于长方形的面积减去四分之一圆的面积。
图形B的面积等于四分之一圆的面积。
显然,图形A的面积大于图形B的面积。
答案:A;B。
四、求下面各图形中阴影部分的周长和面积。(单位:cm)(10分)
1. (5分)
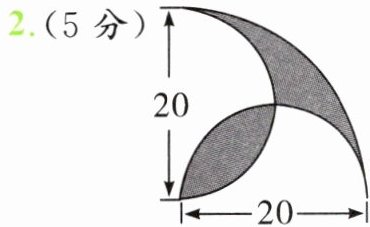
2. (5分)
1. (5分)

2. (5分)

答案:
1. 周长:3.14×4×2÷2 + 3.14×4÷2 = 18.84(cm)
面积:3.14×4²÷2 - 3.14×(4÷2)²÷2 = 18.84(cm²)
2. 周长:3.14×20×2÷4 + 3.14×20 = 94.2(cm)
面积:3.14×20²÷4 - 20×20÷2 = 114(cm²)
面积:3.14×4²÷2 - 3.14×(4÷2)²÷2 = 18.84(cm²)
2. 周长:3.14×20×2÷4 + 3.14×20 = 94.2(cm)
面积:3.14×20²÷4 - 20×20÷2 = 114(cm²)
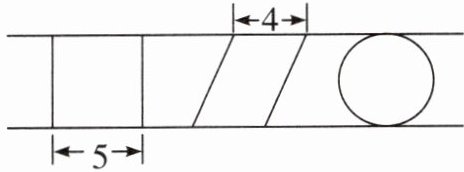
1. 如下图,平行四边形的面积是$24cm^{2}$,求其他两个图形的面积。(单位:cm)(8分)

答案:
答案略
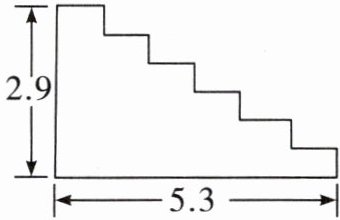
2. 盛大公司准备在新建的办公楼大厅的主楼梯上面铺红地毯,已知这种红地毯每平方米的售价是40元,主楼梯宽2.5 m,其侧面如下图所示(单位:m)。请你算一算,购买这种红地毯需要多少钱?(8分)

答案:
解析:本题可先通过平移求出铺红地毯部分的面积,再根据每平方米红地毯的售价求出总花费。
将楼梯的水平线段向上平移,竖直线段向右平移,可发现铺红地毯的部分展开后是一个长方形。
这个长方形的长为楼梯的竖直高度与水平长度之和,宽为楼梯的宽度。
已知楼梯宽$2.5m$,竖直高度为$2.9m$,水平长度为$5.3m$,则红地毯的长度为:
$2.9 + 5.3 = 8.2$($m$)
根据长方形的面积公式$S = a× b$(其中$S$为长方形面积,$a$为长方形的长,$b$为长方形的宽),可得红地毯的面积为:
$8.2×2.5 = 20.5$($m^2$)
已知这种红地毯每平方米的售价是$40$元,根据“总价 = 单价×数量”,可得购买这种红地毯需要:
$20.5×40 = 820$(元)
答案:
红地毯的长:$2.9 + 5.3 = 8.2$($m$)
红地毯的面积:$8.2×2.5 = 20.5$($m^2$)
购买红地毯需要的钱数:$20.5×40 = 820$(元)
答:购买这种红地毯需要$820$元。
将楼梯的水平线段向上平移,竖直线段向右平移,可发现铺红地毯的部分展开后是一个长方形。
这个长方形的长为楼梯的竖直高度与水平长度之和,宽为楼梯的宽度。
已知楼梯宽$2.5m$,竖直高度为$2.9m$,水平长度为$5.3m$,则红地毯的长度为:
$2.9 + 5.3 = 8.2$($m$)
根据长方形的面积公式$S = a× b$(其中$S$为长方形面积,$a$为长方形的长,$b$为长方形的宽),可得红地毯的面积为:
$8.2×2.5 = 20.5$($m^2$)
已知这种红地毯每平方米的售价是$40$元,根据“总价 = 单价×数量”,可得购买这种红地毯需要:
$20.5×40 = 820$(元)
答案:
红地毯的长:$2.9 + 5.3 = 8.2$($m$)
红地毯的面积:$8.2×2.5 = 20.5$($m^2$)
购买红地毯需要的钱数:$20.5×40 = 820$(元)
答:购买这种红地毯需要$820$元。
3. 四季园小区居民公共活动室内要铺设一条人行甬道,甬道长80 m,宽1.6 m。现在用边长都是0.4 m的红、黄两种正方形地砖铺设(下面是铺设的甬道局部图,其中空白部分表示黄色,灰底部分表示红色)。(14分)


(1)铺设这条人行甬道一共需要多少块地砖?(7分)
(2)铺设这条人行甬道一共需要多少块红色地砖?(7分)


(1)铺设这条人行甬道一共需要多少块地砖?(7分)
(2)铺设这条人行甬道一共需要多少块红色地砖?(7分)
答案:
(1)甬道面积:80×1.6=128(m²)
地砖面积:0.4×0.4=0.16(m²)
总地砖数:128÷0.16=800(块)
(2)甬道宽度方向地砖数:1.6÷0.4=4(块)
局部图横向地砖数:观察得为4块(2红2黄一组循环)
每组长度:4×0.4=1.6(m)
总组数:80÷1.6=50(组)
每组红色地砖数:2×2=4(块)
红色地砖总数:50×4=200(块)
(1)800块
(2)200块
(1)甬道面积:80×1.6=128(m²)
地砖面积:0.4×0.4=0.16(m²)
总地砖数:128÷0.16=800(块)
(2)甬道宽度方向地砖数:1.6÷0.4=4(块)
局部图横向地砖数:观察得为4块(2红2黄一组循环)
每组长度:4×0.4=1.6(m)
总组数:80÷1.6=50(组)
每组红色地砖数:2×2=4(块)
红色地砖总数:50×4=200(块)
(1)800块
(2)200块
查看更多完整答案,请扫码查看


