《2025年暑假集训合肥工业大学出版社六年级数学人教版》

例 一个圆柱的侧面沿高展开图正好是一个边长为 31.4 cm 的正方形,求它的表面积。
【分析】 圆柱的侧面沿高展开是正方形,则圆柱的底面周长$(C)= 圆柱的高(h)$,先根据公式$r= \frac {C}{2π}$求出半径(r),即$31.4÷(3.14×2)= 5(cm)$,再根据公式$S= πr^{2}$求出圆柱的底面积(S),即$3.14×5^{2}= 78.5(cm^{2})$,最后再求出表面积。
【答案】$31.4×31.4+3.14×(31.4÷3.14÷2)^{2}×2= 1142.96(cm^{2})$
答：它的表面积是$1142.96cm^{2}$。
【点拨】 此题考查圆柱的侧面展开图及表面积的计算。

答案： 【分析】
圆柱的侧面沿高展开是正方形，说明圆柱的底面周长$C$等于圆柱的高$h$。
先根据公式$r = \frac{C}{2\pi}$求出底面半径$r$，再根据公式$S=\pi r^{2}$求出圆柱的底面积$S$，最后根据圆柱表面积公式$S_{表}=S_{侧}+2S_{底}$求出表面积，其中$S_{侧}=Ch$（$C$为底面周长，$h$为高）。
【解答】
半径：
$31.4÷3.14÷2$
$=10÷2$
$ = 5(cm)$
底面积：
$3.14×5^{2}$
$=3.14×25$
$ = 78.5(cm^{2})$
侧面积：
$31.4×31.4 = 985.96(cm^{2})$
表面积：
$985.96+78.5×2$
$=985.96 + 157$
$=1142.96(cm^{2})$
答：它的表面积是$1142.96cm^{2}$。

1.求下面空心圆柱的表面积。(单位:cm)

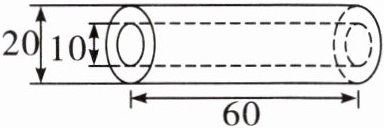
圆柱的表面积

答案： 3.14×10×60+3.14×20×60+3.14×[${\left( \dfrac{20}{2}\right)}^{2}-{\left( \dfrac{10}{2}\right)}^{2}$]×2=6123($\text{cm}^2$)

2.一个圆柱的底面周长和高相等,如果高缩短 2 cm,表面积就减少$12.56cm^{2}$,求这个圆柱的表面积。

答案： 12.56÷2÷3.14÷2=1($\text{cm}$) 3.14×${1}^{2}$×2+(3.14×1×2)${}^{2}$=45.7184($\text{cm}^2$)

3.将一个圆柱的侧面展开,得到一个正方形,已知这个正方形的周长是 62.8 cm,则这个圆柱的表面积是多少平方厘米？

答案： 62.8÷4=15.7($\text{cm}$) 15.7÷3.14÷2=2.5($\text{cm}$)
3.14×${2.5}^{2}$×2+15.7×15.7=285.74($\text{cm}^2$)

4.用铁皮制作一个圆柱形油桶,底面半径是 5 dm,高的长度与底面半径的比是$4:1$,制作这个油桶至少需要铁皮多少平方分米？

答案： 3.14×5×2×5×4+3.14×${5}^{2}$×2=785($\text{dm}^2$)