《2025年通城学典小升初真题汇编数学》

13. ( ):20= $\frac{4}{5}$= 24÷( )= ( )%= ( )(填小数)

答案： 16 30 80 0.8

14. (1)下图中的直线上,点 A 表示的数是( );点 C 表示的数是$\frac{5}{2}$,在直线上标出点 C。
(2)下图中 OB 所在的四边形是正方形。以 O 为圆心,OB 长为半径作如图所示的扇形。估一估,正方形对角线 OB 的长大约是边长的( )倍(用一位小数表示)。

答案： （1）-3；（2）1.4（合理即可）

15. 分数单位是$\frac{1}{6}$的最简真分数有( )个;分数$\frac{A}{6}和\frac{10}{A}$都是分数值小于 2 的最简分数,A 的值是( )。

答案： 2 7 或 11

16. 小明用竖式计算一个数乘 36 时,不小心将其中一部分污损了(如图)。A 部分的数值是 B 部分的数值的$\frac{( )}{( )}$,A 部分的数值与 C 部分的比是( : )。

答案： $\frac{1}{5}$ 1:6

17. 世界卫生组织提出男生标准体重的计算方法是“标准体重(千克)= [身高(厘米)-80]×70%”。六年级的平平身高 150 厘米,体重 60 千克。他的标准体重应是( )千克。下表是人的不同体重状况的参考标准,平平的体重状况是( )。
|体重状况|正常体重|超重|轻度肥胖|中度肥胖|重度肥胖|
|参考标准|不超出标准体重的 10%|超出标准体重的 10%~20%|超出标准体重的 20%~30%|超出标准体重的 30%~40%|超出标准体重的 40%|

答案： 49 轻度肥胖

18. 等底等高的图形在数学知识的学习中有着重要的作用。
(1)把一个圆柱平均分成若干份,拼成一个等底等高的长方体(如右图),长方体的宽是 2 分米,高是 3 分米,长方体的长是( )分米,圆柱的体积是( )立方分米。
(2)如果一个圆柱和圆锥等底等高,同时圆柱的体积比圆锥多 50 立方分米,那么这个圆柱的体积是( )立方分米。
(3)等底等高的平行四边形和三角形,如果它们的面积之和是 36 平方厘米,它们的底都是 10 厘米,那么它们的高都是( )厘米。

答案： （1）6.28 37.68；（2）75；（3）2.4

19. 古希腊著名的毕达哥拉斯学派对“三角形数、正方形数、五边形数”等有所研究。
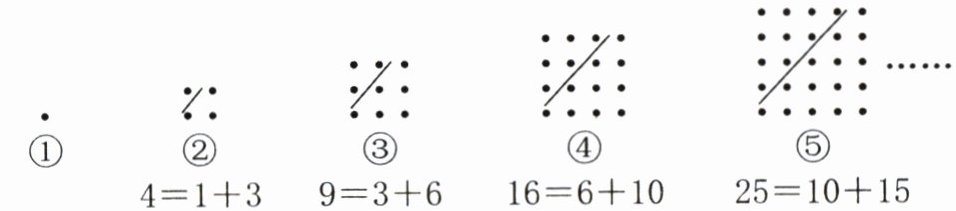
(1)他们把 1、3、6、10、15……这样的数称作“三角形数”(如图)。第 6 个“三角形数”是( );第 n 个“三角形数”是( )。
(2)他们把 1、4、9、16……这样的数称作“正方形数”(如图)。第 n 个“正方形数”是( )。
(3)如果用一条斜线把“正方形数”分成了两部分(如图),那么可以发现任何一个大于 1 的“正方形数”都可以看作两个相邻的“三角形数”之和。以此类推,第⑤幅图为( )= ( )+( )。

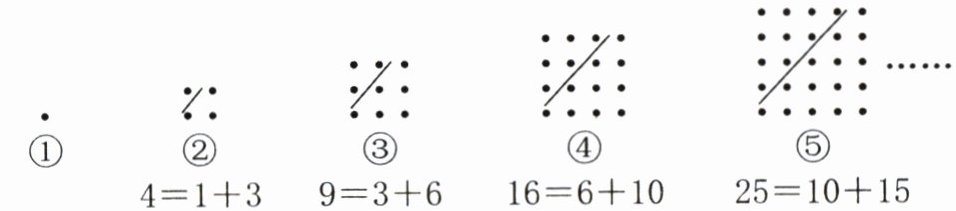
答案： （1）21 $\frac{(1+n)n}{2}$；（2）$n^2$；（3）$n^2$ $\frac{n(n - 1)}{2}$ $\frac{(1+n)n}{2}$