《2025年中考快递同步检测九年级数学全一册人教版》

16. 新考向 综合与实践 在“综合与实践”课上，同学们以“图形的旋转”为主题开展数学活动.
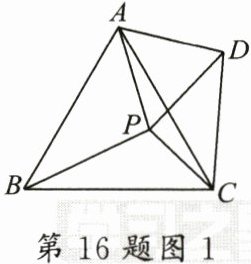
（1）探究发现：如图1，在等边△ABC的内部有一点P，连接AP，BP，CP，将线段AP绕点A逆时针旋转60°，得到线段AD，连接PD，CD，若AP² + CP² = BP²，则∠APC的度数是_______；
（2）类比延伸：如图2，在△ABC中，AB = AC，∠BAC = 90°. 在△ABC的内部有一点P，连接AP，BP，CP，若∠APC = 135°，试判断AP，BP，CP之间的数量关系，并说明理由；
（3）迁移应用：如图3，在△ABC中，AB = AC，∠BAC = 120°. 在直线AC上方有一点P，连接AP，BP，CP，若∠APC = 60°，则存在实数m使得mAP² + CP² = BP²成立，请直接写出m的值.
　　

答案：
解：
(1)$150^{\circ}$
(2)$2AP^{2}+CP^{2}=BP^{2}$. 理由如下：
如图1，将$\triangle APB$绕点$A$逆时针旋转$90^{\circ}$得到$\triangle ATC$，连接$PT$.
　　　　　　　
根据旋转性质，得$AP = AT$，$\angle PAT = 90^{\circ}$，$CT = BP$.
$\therefore\angle APT=\angle ATP = 45^{\circ}$.
在$Rt\triangle APT$中，根据勾股定理，得
$PT=\sqrt{AP^{2}+AT^{2}}=\sqrt{2AP^{2}}=\sqrt{2}AP$.
$\because\angle APC = 135^{\circ}$，
$\therefore\angle TPC=\angle APC-\angle APT = 135^{\circ}-45^{\circ}=90^{\circ}$.
在$Rt\triangle CPT$中，根据勾股定理，$PT^{2}+CP^{2}=CT^{2}$.
$\therefore(\sqrt{2}AP)^{2}+CP^{2}=BP^{2}$. $\therefore 2AP^{2}+CP^{2}=BP^{2}$.
(3)$m$的值为$3$.
解析：如图2，将$\triangle ACP$绕点$A$顺时针旋转$120^{\circ}$得到$\triangle ABQ$，连接$PQ$，过点$A$作$AH\perp PQ$，垂足为$H$.
根据旋转的性质，得$AP = AQ$，$\angle PAQ=\angle BAC = 120^{\circ}$，$CP = BQ$，$\angle APC=\angle AQB = 60^{\circ}$.
$\therefore\angle PQA=\angle APQ=\frac{180^{\circ}-120^{\circ}}{2}=30^{\circ}$.
$\therefore\angle BQP=\angle PQA+\angle AQB = 30^{\circ}+60^{\circ}=90^{\circ}$.
在$Rt\triangle PBQ$中，根据勾股定理，$PQ^{2}+BQ^{2}=BP^{2}$.
$\because AP = AQ$，$AH\perp PQ$，$\therefore PQ = 2PH$.
在$Rt\triangle APH$中，$\because\angle APQ = 30^{\circ}$，$\therefore AH=\frac{1}{2}AP$.
根据勾股定理，得$PH=\sqrt{AP^{2}-AH^{2}}=\frac{\sqrt{3}}{2}AP$.
$\therefore PQ=\sqrt{3}AP$. $\therefore 3AP^{2}+CP^{2}=BP^{2}$.
$\because mAP^{2}+CP^{2}=BP^{2}$，$\therefore m$的值为$3$.