19. (12分)如图,$AB = AD$,$BC = DC$,点$E$在$AC$上,连接$BE$,$DE$.
(1)求证:$AC$平分$\angle BAD$.
(2)求证:$EB = ED$.

(1)求证:$AC$平分$\angle BAD$.
(2)求证:$EB = ED$.

答案:
19.证明:
(1)在△ABC和△ADC中,$\begin{cases}AC=AC,\\BC=DC,\\\end{cases}$
∴△ABC≌△ADC(SSS).
∴∠BAC=∠DAC.
∴AC平分∠BAD.
(2)在△ABE和△ADE中,$\begin{cases}AB=AD,\\∠BAE=∠DAE,\\AE=AE,\end{cases}$
∴△ABE≌△ADE(SAS).
∴EB=ED.
(1)在△ABC和△ADC中,$\begin{cases}AC=AC,\\BC=DC,\\\end{cases}$
∴△ABC≌△ADC(SSS).
∴∠BAC=∠DAC.
∴AC平分∠BAD.
(2)在△ABE和△ADE中,$\begin{cases}AB=AD,\\∠BAE=∠DAE,\\AE=AE,\end{cases}$
∴△ABE≌△ADE(SAS).
∴EB=ED.
20. (13分)【初步探索】
(1)如图1,在四边形$ABCD$中,$AB = AD$,$\angle B = \angle ADC = 90°$,点$E$,$F$分别是$BC$,$CD$上的点,连接$AE$,$AF$,$EF$,且$EF = BE + FD$.探究图中$\angle EAF$,$\angle BAE$,$\angle FAD$之间的数量关系.
小明探究此问题的方法如下:延长$FD$至点$G$,使$DG = BE$,连接$AG$.先证明$\triangle ABE \cong \triangle ADG$,再证明$\triangle AEF \cong \triangle AGF$,即可得出结论.他的结论是
【灵活运用】
(2)如图2,在四边形$ABCD$中,$AB = AD$,$\angle B + \angle D = 180°$,点$E$,$F$分别是$BC$,$CD$上的点,且$EF = BE + FD$.请判断(1)中的结论是否仍然成立,并说明理由.
【拓展延伸】
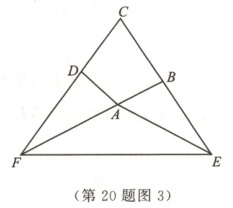
(3)如图3,在四边形$ABCD$中,$\angle ABC + \angle ADC = 180°$,$AB = AD$.点$E$在$CB$的延长线上,点$F$在$CD$的延长线上,且$EF = BE + FD$.若$\angle ECF = 70°$,请直接写出$\angle EAF$的度数.


(1)如图1,在四边形$ABCD$中,$AB = AD$,$\angle B = \angle ADC = 90°$,点$E$,$F$分别是$BC$,$CD$上的点,连接$AE$,$AF$,$EF$,且$EF = BE + FD$.探究图中$\angle EAF$,$\angle BAE$,$\angle FAD$之间的数量关系.
小明探究此问题的方法如下:延长$FD$至点$G$,使$DG = BE$,连接$AG$.先证明$\triangle ABE \cong \triangle ADG$,再证明$\triangle AEF \cong \triangle AGF$,即可得出结论.他的结论是
∠EAF=∠BAE+∠FAD
.【灵活运用】
(2)如图2,在四边形$ABCD$中,$AB = AD$,$\angle B + \angle D = 180°$,点$E$,$F$分别是$BC$,$CD$上的点,且$EF = BE + FD$.请判断(1)中的结论是否仍然成立,并说明理由.
【拓展延伸】
(3)如图3,在四边形$ABCD$中,$\angle ABC + \angle ADC = 180°$,$AB = AD$.点$E$在$CB$的延长线上,点$F$在$CD$的延长线上,且$EF = BE + FD$.若$\angle ECF = 70°$,请直接写出$\angle EAF$的度数.



答案:
20.
(1)∠EAF=∠BAE+∠FAD
【解析】易证△ABE≌△ADG(SAS).
∴∠BAE=∠DAG,AE=AG.
易证△AEF≌△AGF(SSS).
∴∠EAF=∠GAF=∠DAG+∠FAD=∠BAE+∠FAD.
(2)结论仍然成立.
理由:如图1,延长FD至点G,使DG=BE,连接AG.
∵∠B+∠ADF=180°,∠ADG+∠ADF=180°,
∴∠B=∠ADG.
在△ABE和△ADG中,$\begin{cases}AB=AD,\\∠B=∠ADG,\\BE=DG,\end{cases}$
∴△ABE≌△ADG(SAS).
∴∠BAE=∠DAG,AE=AG.
∴EF=BE+FD=DG+FD=GF.
在△AEF和△AGF中,$\begin{cases}AE=AG,\\AF=AF,\\EF=GF,\end{cases}$
∴△AEF≌△AGF(SSS).
∴∠EAF=∠GAF.
∵∠GAF=∠DAG+∠FAD=∠BAE+∠FAD,
∴∠EAF=∠BAE+∠FAD.
(3)∠EAF=125°.
【解析】如图2,在DC的延长线上取一点G,使DG=BE,连接AG.
∵∠ABC+∠ADC=180°,∠ABC+∠ABE=180°,
∴∠ADC=∠ABE.
易证△ADG≌△ABE(SAS).
∴AG=AE,∠G=∠BEA.
易证△AEF≌△AGF(SSS).
∴∠G=∠FEA,∠GFA=∠EFA=$\frac{1}{2}$∠CFE.
∴∠BEA=∠FEA=$\frac{1}{2}$∠CEF.
在△EAF中,∠EAF=180°-(∠EFA+∠FEA)=180°-$\frac{1}{2}$(∠CFE+∠CEF)=180°-$\frac{1}{2}$(180°-∠ECF)=90°+$\frac{1}{2}$∠ECF.
∵∠ECF=70°,
∴∠EAF=125°.
(1)∠EAF=∠BAE+∠FAD
【解析】易证△ABE≌△ADG(SAS).
∴∠BAE=∠DAG,AE=AG.
易证△AEF≌△AGF(SSS).
∴∠EAF=∠GAF=∠DAG+∠FAD=∠BAE+∠FAD.
(2)结论仍然成立.
理由:如图1,延长FD至点G,使DG=BE,连接AG.
∵∠B+∠ADF=180°,∠ADG+∠ADF=180°,
∴∠B=∠ADG.
在△ABE和△ADG中,$\begin{cases}AB=AD,\\∠B=∠ADG,\\BE=DG,\end{cases}$
∴△ABE≌△ADG(SAS).
∴∠BAE=∠DAG,AE=AG.
∴EF=BE+FD=DG+FD=GF.
在△AEF和△AGF中,$\begin{cases}AE=AG,\\AF=AF,\\EF=GF,\end{cases}$
∴△AEF≌△AGF(SSS).
∴∠EAF=∠GAF.
∵∠GAF=∠DAG+∠FAD=∠BAE+∠FAD,
∴∠EAF=∠BAE+∠FAD.
(3)∠EAF=125°.
【解析】如图2,在DC的延长线上取一点G,使DG=BE,连接AG.
∵∠ABC+∠ADC=180°,∠ABC+∠ABE=180°,
∴∠ADC=∠ABE.
易证△ADG≌△ABE(SAS).
∴AG=AE,∠G=∠BEA.
易证△AEF≌△AGF(SSS).
∴∠G=∠FEA,∠GFA=∠EFA=$\frac{1}{2}$∠CFE.
∴∠BEA=∠FEA=$\frac{1}{2}$∠CEF.
在△EAF中,∠EAF=180°-(∠EFA+∠FEA)=180°-$\frac{1}{2}$(∠CFE+∠CEF)=180°-$\frac{1}{2}$(180°-∠ECF)=90°+$\frac{1}{2}$∠ECF.
∵∠ECF=70°,
∴∠EAF=125°.
查看更多完整答案,请扫码查看


