《2025年点石成金金牌夺冠八年级数学上册人教版辽宁专版》

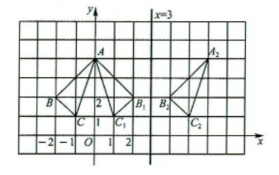
17. (10分)△ABC在平面直角坐标系中的位置如图所示.
(1)画出△ABC关于y轴对称的图形△$AB_1C_1$，并直接写出点A，$B_1$，$C_1$的坐标.
(2)将△ABC向右平移6个单位长度，画出平移后的图形△$A_2B_2C_2$.
(3)△$AB_1C_1$和△$A_2B_2C_2$是否关于某条直线对称？若是，请在图中画出这条直线；若不是，请说明理由.

答案：
17.
(1)如图. 点$A(0,4)$,$B_1(2,2)$,$C_1(1,1)$.
(2)如图.
(3)$\triangle AB_1C_1$和$\triangle A_2B_2C_2$关于直线$x=3$对称.

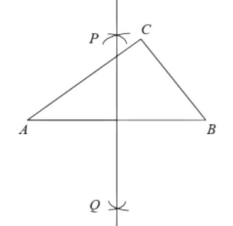
18. (10分)如图，在△ABC中，AC ＞ BC.
(1)尺规作图：作AB的垂直平分线交AC于点P.(保留作图痕迹，不写作法)
(2)连接PB.若AB = 8，△PBC的周长是13，求△ABC的周长.
(3)在(2)的条件下，若△ABC是等腰三角形，直接写出△ABC的三条边AB，AC，BC的长.

答案：
18.
(1)
(2)解：$\because$点$P$在$AB$的垂直平分线上,$\therefore PA=PB$.
$\therefore AC=PA+PC=PB+PC$.
$\therefore C_{\triangle ABC}=AB+AC+BC=AB+PB+PC+BC$.
$\because C_{\triangle PBC}=PB+PC+BC=13$,$AB=8$,
$\therefore C_{\triangle ABC}=AB+C_{\triangle PBC}=8+13=21$.
(3)$AB=8$,$AC=8$,$BC=5$.

19. (12分)如图1，已知△ABC是等边三角形，过点C作CD//AB，连接BD，交AC于点O，且OA = OC.
(1)求证：AC垂直平分BD.
(2)如图2，点M在BC的延长线上，点N在线段CO上，连接NB，ND，NM，且ND = NM，求证：NB = NM.

答案： 19.证明：
(1)$\because \triangle ABC$是等边三角形,$OA=OC$,
$\therefore BO\perp AC$.
$\because CD// AB$,$\therefore \angle A=\angle OCD$.
在$\triangle BOA$和$\triangle DOC$中,$\begin{cases}\angle BOA=\angle DOC,\\OA=OC,\\\angle A=\angle OCD,\end{cases}$
$\therefore \triangle BOA\cong\triangle DOC(ASA).\therefore BO=DO$.
$\because BO\perp AC$,$\therefore AC$垂直平分$BD$.
(2)由
(1)得,$AC$垂直平分$BD.\therefore NB=ND$.
$\because ND=NM$,$\therefore NB=NM$.