17. (10分)如图,在△ABC中,作AC边的垂直平分线MN交BC于点D,连接AD.
(1)根据题意补全图形. (保留作图痕迹,不写作法)
(2)若AB = AD,∠BAD = 40°,求∠C的度数.

(1)根据题意补全图形. (保留作图痕迹,不写作法)
(2)若AB = AD,∠BAD = 40°,求∠C的度数.

答案:
17.
(1)如图,即为所求.

(2)解:$\because AB = AD$,$\angle BAD = 40^{\circ}$,
$\therefore \angle B = \angle 1 = \frac{1}{2}(180^{\circ} - \angle BAD) = 70^{\circ}$.
$\because MN$垂直平分AC,$\therefore AD = CD$.$\therefore \angle C = \angle 2$.
$\because \angle 1 = \angle C + \angle 2$,$\therefore \angle C = \frac{1}{2} \angle 1 = 35^{\circ}$.
17.
(1)如图,即为所求.

(2)解:$\because AB = AD$,$\angle BAD = 40^{\circ}$,
$\therefore \angle B = \angle 1 = \frac{1}{2}(180^{\circ} - \angle BAD) = 70^{\circ}$.
$\because MN$垂直平分AC,$\therefore AD = CD$.$\therefore \angle C = \angle 2$.
$\because \angle 1 = \angle C + \angle 2$,$\therefore \angle C = \frac{1}{2} \angle 1 = 35^{\circ}$.
18. (8分)如图,已知△ABC三个顶点的坐标分别是点A(-5,0),B(-2,4),C(-1,-2),△A'B'C'与△ABC关于y轴对称.
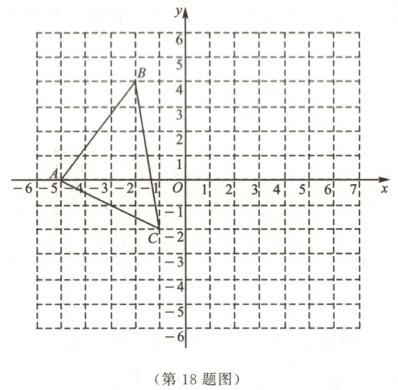
(1)直接写出点A',B',C'的坐标.
(2)在图中画出△A'B'C'.
(3)求△ABC的面积.

(1)直接写出点A',B',C'的坐标.
(2)在图中画出△A'B'C'.
(3)求△ABC的面积.
答案:
18.
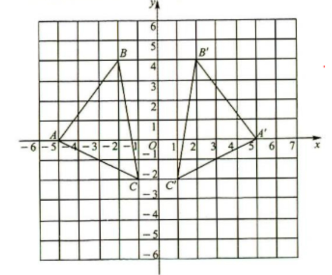
(1)点$A'(5,0)$,$B'(2,4)$,$C'(1,-2)$.
(2)
(3)解:$S_{\triangle ABC} = 4 × 6 - \frac{1}{2} × 3 × 4 - \frac{1}{2} × 2 × 4 - \frac{1}{2} × 1 × 6 = 11$.
$\therefore \triangle ABC$的面积是11.
18.
(1)点$A'(5,0)$,$B'(2,4)$,$C'(1,-2)$.
(2)

(3)解:$S_{\triangle ABC} = 4 × 6 - \frac{1}{2} × 3 × 4 - \frac{1}{2} × 2 × 4 - \frac{1}{2} × 1 × 6 = 11$.
$\therefore \triangle ABC$的面积是11.
查看更多完整答案,请扫码查看


