20. (13分)综合与实践.
【问题情境】
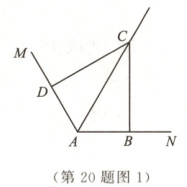
数学活动课上,王老师提出了一个问题:如图1,$ \angle MAN = 120°$,AC平分$ \angle MAN$,CD⊥AM于点D,CB⊥AN于点B.若AC = 4,求AB + AD的长.
【独立思考】
(1)请解答王老师提出的问题.
【深入探究】
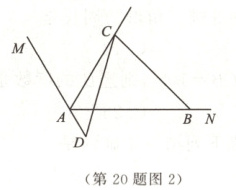
(2)在解决了王老师提出的问题后,小聪发现,若$ \angle DCB$的大小不变,点D在MA的延长线上,点B在射线AN上,其余条件不变,则线段AB,AD,AC之间具有一定的数量关系,请你猜想并说明理由.
【扩展实践】
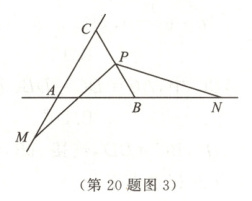
(3)数学活动小组的同学对上述问题进行特殊化研究,提出了新的问题,请你解答:如图3,△ABC是等边三角形,AB = 8,点P是BC的中点,射线PM与直线AC交于点M,射线PN与直线AB交于点N,$ \angle MPN = 120°$.当AM = 5时,求AN的长.
【问题情境】
数学活动课上,王老师提出了一个问题:如图1,$ \angle MAN = 120°$,AC平分$ \angle MAN$,CD⊥AM于点D,CB⊥AN于点B.若AC = 4,求AB + AD的长.
【独立思考】
(1)请解答王老师提出的问题.
【深入探究】
(2)在解决了王老师提出的问题后,小聪发现,若$ \angle DCB$的大小不变,点D在MA的延长线上,点B在射线AN上,其余条件不变,则线段AB,AD,AC之间具有一定的数量关系,请你猜想并说明理由.
【扩展实践】
(3)数学活动小组的同学对上述问题进行特殊化研究,提出了新的问题,请你解答:如图3,△ABC是等边三角形,AB = 8,点P是BC的中点,射线PM与直线AC交于点M,射线PN与直线AB交于点N,$ \angle MPN = 120°$.当AM = 5时,求AN的长.



答案:
20.
(1)解:$\because \angle MAN=120^{\circ}$,$AC$平分$\angle MAN$,
$\therefore \angle CAD=\angle CAB=\frac{1}{2}\angle MAN=60^{\circ}$.
$\because CD\perp AM$,$CB\perp AN$,$\therefore \angle ADC=\angle ABC=90^{\circ}$.
$\therefore \angle ACD=\angle ACB=30^{\circ}.\therefore AC=2AD=2AB=4$.
$\therefore AB=AD=2.\therefore AB+AD=4$.
(2)$AB - AD=AC$.
理由:如图1,过点$C$分别作$CE\perp AM$于点$E$,$CF\perp AN$于点$F$.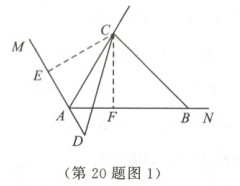
$\because \angle MAN=120^{\circ}$,$AC$平分$\angle MAN$,
$\therefore \angle EAC=\angle FAC=60^{\circ}$,$CE=CF$.
由
(1)得,$\angle ECF=60^{\circ}$,$AC=2AF=2AE$.
$\because \angle DCB=60^{\circ}$,$\therefore \angle ECF=\angle DCB$.
$\therefore \angle ECF - \angle DCF=\angle DCB - \angle DCF$,
即$\angle ECD=\angle FCB$.
在$\triangle ECD$和$\triangle FCB$中,$\begin{cases}\angle CED=\angle CFB,\\CE=CF,\\\angle ECD=\angle FCB,\end{cases}$
$\therefore \triangle ECD\cong\triangle FCB(ASA).\therefore ED=FB$.
$\therefore AB - AD=AF+FB - AD=AF+ED - AD=AF+AE=2AF=AC$.
(3)解:①当点$M$在$CA$的延长线上时,如图2,连接$AP$,在$BN$上取点$G$,使$BG=BP$,连接$PG$,过点$P$作$PH\perp AN$于点$H$.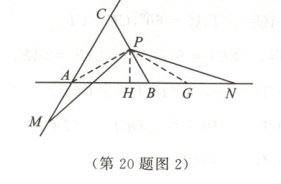
$\because \triangle ABC$是等边三角形,点$P$是$BC$的中点,
$\therefore BP=\frac{1}{2}BC=\frac{1}{2}AB=4$,$\angle ABC=60^{\circ}$,$AP\perp BC$,$\angle PAC=\angle PAB=30^{\circ}$.
$\because BG=BP$,$\therefore \angle BGP=\angle BPG=\frac{1}{2}\angle ABC=30^{\circ}$.
$\therefore \angle PAG=\angle PGA.\therefore PA=PG$,$\angle APG=120^{\circ}$.
$\because \angle MPN=120^{\circ}$,
$\therefore \angle APG - \angle MPG=\angle MPN - \angle MPG$,
即$\angle APM=\angle GPN$.
$\because \angle PAC=\angle PGA=30^{\circ}$,$\angle PAC+\angle PAM=180^{\circ}$,$\angle PGA+\angle PGN=180^{\circ}$,$\therefore \angle PAM=\angle PGN$.
在$\triangle PAM$和$\triangle PGN$中,$\begin{cases}\angle APM=\angle GPN,\\PA=PG,\\\angle PAM=\angle PGN,\end{cases}$
$\therefore \triangle PAM\cong\triangle PGN(ASA).\therefore AM=GN=5$.
$\therefore AN=AB+BG+GN=AB+BP+AM=8+4+5=17$.
②当点$M$在线段$AC$上时,如图3,连接$AP$,取$AB$的中点$G$,连接$PG$.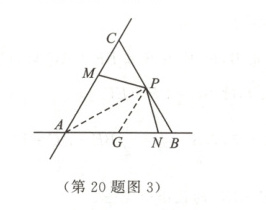
$\because$点$G$是$AB$的中点,点$P$是$BC$的中点,
$\therefore AG=BG=\frac{1}{2}AB$,$BP=\frac{1}{2}BC$.
$\because AB=BC=8$,$\therefore AG=BG=BP=4$.
$\because \angle PBG=60^{\circ}$,$\therefore \triangle PBG$是等边三角形.
$\therefore \angle BPG=\angle PGN=60^{\circ}$,$PG=PB=PC$.
$\therefore \angle GPC=180^{\circ}-\angle GPB=120^{\circ}$.
$\because \angle MPN=120^{\circ}$,$\therefore \angle GPC=\angle MPN$.
$\therefore \angle GPC - \angle GPM=\angle MPN - \angle GPM$,
即$\angle CPM=\angle GPN$.
在$\triangle CPM$和$\triangle GPN$中,$\begin{cases}\angle PCM=\angle PGN,\\PC=PG,\\\angle CPM=\angle GPN,\end{cases}$
$\therefore \triangle CPM\cong\triangle GPN(ASA)$.
$\therefore CM=GN=AC - AM=8 - 5=3$.
$\therefore AN=AG+GN=4+3=7$.
综上所述,$AN$的长是17或7.
20.
(1)解:$\because \angle MAN=120^{\circ}$,$AC$平分$\angle MAN$,
$\therefore \angle CAD=\angle CAB=\frac{1}{2}\angle MAN=60^{\circ}$.
$\because CD\perp AM$,$CB\perp AN$,$\therefore \angle ADC=\angle ABC=90^{\circ}$.
$\therefore \angle ACD=\angle ACB=30^{\circ}.\therefore AC=2AD=2AB=4$.
$\therefore AB=AD=2.\therefore AB+AD=4$.
(2)$AB - AD=AC$.
理由:如图1,过点$C$分别作$CE\perp AM$于点$E$,$CF\perp AN$于点$F$.

$\because \angle MAN=120^{\circ}$,$AC$平分$\angle MAN$,
$\therefore \angle EAC=\angle FAC=60^{\circ}$,$CE=CF$.
由
(1)得,$\angle ECF=60^{\circ}$,$AC=2AF=2AE$.
$\because \angle DCB=60^{\circ}$,$\therefore \angle ECF=\angle DCB$.
$\therefore \angle ECF - \angle DCF=\angle DCB - \angle DCF$,
即$\angle ECD=\angle FCB$.
在$\triangle ECD$和$\triangle FCB$中,$\begin{cases}\angle CED=\angle CFB,\\CE=CF,\\\angle ECD=\angle FCB,\end{cases}$
$\therefore \triangle ECD\cong\triangle FCB(ASA).\therefore ED=FB$.
$\therefore AB - AD=AF+FB - AD=AF+ED - AD=AF+AE=2AF=AC$.
(3)解:①当点$M$在$CA$的延长线上时,如图2,连接$AP$,在$BN$上取点$G$,使$BG=BP$,连接$PG$,过点$P$作$PH\perp AN$于点$H$.

$\because \triangle ABC$是等边三角形,点$P$是$BC$的中点,
$\therefore BP=\frac{1}{2}BC=\frac{1}{2}AB=4$,$\angle ABC=60^{\circ}$,$AP\perp BC$,$\angle PAC=\angle PAB=30^{\circ}$.
$\because BG=BP$,$\therefore \angle BGP=\angle BPG=\frac{1}{2}\angle ABC=30^{\circ}$.
$\therefore \angle PAG=\angle PGA.\therefore PA=PG$,$\angle APG=120^{\circ}$.
$\because \angle MPN=120^{\circ}$,
$\therefore \angle APG - \angle MPG=\angle MPN - \angle MPG$,
即$\angle APM=\angle GPN$.
$\because \angle PAC=\angle PGA=30^{\circ}$,$\angle PAC+\angle PAM=180^{\circ}$,$\angle PGA+\angle PGN=180^{\circ}$,$\therefore \angle PAM=\angle PGN$.
在$\triangle PAM$和$\triangle PGN$中,$\begin{cases}\angle APM=\angle GPN,\\PA=PG,\\\angle PAM=\angle PGN,\end{cases}$
$\therefore \triangle PAM\cong\triangle PGN(ASA).\therefore AM=GN=5$.
$\therefore AN=AB+BG+GN=AB+BP+AM=8+4+5=17$.
②当点$M$在线段$AC$上时,如图3,连接$AP$,取$AB$的中点$G$,连接$PG$.

$\because$点$G$是$AB$的中点,点$P$是$BC$的中点,
$\therefore AG=BG=\frac{1}{2}AB$,$BP=\frac{1}{2}BC$.
$\because AB=BC=8$,$\therefore AG=BG=BP=4$.
$\because \angle PBG=60^{\circ}$,$\therefore \triangle PBG$是等边三角形.
$\therefore \angle BPG=\angle PGN=60^{\circ}$,$PG=PB=PC$.
$\therefore \angle GPC=180^{\circ}-\angle GPB=120^{\circ}$.
$\because \angle MPN=120^{\circ}$,$\therefore \angle GPC=\angle MPN$.
$\therefore \angle GPC - \angle GPM=\angle MPN - \angle GPM$,
即$\angle CPM=\angle GPN$.
在$\triangle CPM$和$\triangle GPN$中,$\begin{cases}\angle PCM=\angle PGN,\\PC=PG,\\\angle CPM=\angle GPN,\end{cases}$
$\therefore \triangle CPM\cong\triangle GPN(ASA)$.
$\therefore CM=GN=AC - AM=8 - 5=3$.
$\therefore AN=AG+GN=4+3=7$.
综上所述,$AN$的长是17或7.
查看更多完整答案,请扫码查看


