《2025年点石成金金牌夺冠八年级数学上册人教版辽宁专版》

22. (12分)如图，在△ABC中，AB = AC，点D是直线BC上一点，以AD为边在AD的右侧作△ADE，使AE = AD，且∠DAE = ∠BAC，连接CE.
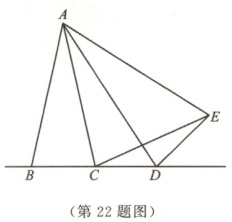
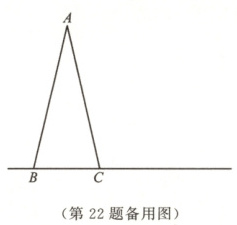
(1)当点D在BC的延长线上移动时，若∠BAC = 25°，则∠DCE的度数是 $25^{\circ}$.
(2)设∠BAC = $\alpha$，∠DCE = $\beta$.
①当点D在BC的延长线上移动时，猜想$\alpha$与$\beta$之间的数量关系，并说明理由.
②当点D在直线BC上移动时(不与B，C两点重合)，猜想$\alpha$与$\beta$之间的数量关系，并直接写出你的结论.

答案：
22.
(1)$25^{\circ}$
(2)①$\alpha = \beta$.
理由：$\because \angle BAC = \angle DAE$，
$\therefore \angle BAC + \angle CAD = \angle DAE + \angle CAD$，
即$\angle BAD = \angle CAE$.
在$\triangle BAD$和$\triangle CAE$中，$\begin{cases} AB = AC, \\ \angle BAD = \angle CAE, \\ AD = AE, \end{cases}$
$\therefore \triangle BAD \cong \triangle CAE (SAS)$.$\therefore \angle ABD = \angle ACE$.
$\because \angle ACD = \angle ABD + \angle BAC = \angle ACE + \angle DCE$，
$\therefore \angle BAC = \angle DCE$.
$\because \angle BAC = \alpha$，$\angle DCE = \beta$，$\therefore \alpha = \beta$.
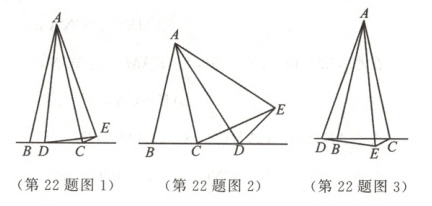
②$\alpha = \beta$或$\alpha + \beta = 180^{\circ}$ [解析]如图1，当点D在线段BC上时，$\alpha + \beta = 180^{\circ}$；如图2，图3，当点D在线段BC的延长线或反向延长线上时，$\alpha = \beta$.