《2025年点石成金金牌夺冠八年级数学上册人教版辽宁专版》

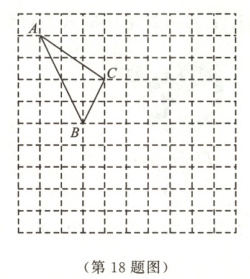
18.(10分)在如图所示的正方形网格中，每个小正方形的边长都为$1$，$\bigtriangleup ABC$的顶点都在网格线的交点上，点$B$关于$y$轴的对称点的坐标为$(2,0)$，点$C$关于$x$轴的对称点的坐标为$(-1,-2)$.
(1)根据上述条件，在网格中建立平面直角坐标系.
(2)画出$\bigtriangleup ABC$关于$y$轴对称的图形$\bigtriangleup A_{1}B_{1}C_{1}$.
(3)直接写出点$A$关于$x$轴的对称点的坐标.

答案：
18.
(1)如图，平面直角坐标系$xOy$即为所求.
(2)如图，$\triangle A_1B_1C_1$即为所求.
(3)点$A$关于$x$轴的对称点的坐标为$(-4,-4)$.

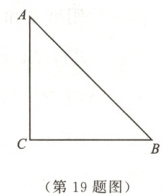
19.(8分)如图，在$\bigtriangleup ABC$中，$AC = BC$，$\angle C = 90^{\circ}$.
(1)尺规作图：在$BC$边上确定一点$D$，使点$D$到$AC$和$AB$的距离相等.(保留作图痕迹，不写作法)
(2)猜想$AB$，$AC$，$CD$之间的数量关系，并证明.

答案：
19.解：
(1)如图1，点$D$即为所求.
(2)$AB=AC+CD$. 理由：如图2，过点$D$作$DE\perp AB$于点$E$. $\because \angle C=90^{\circ},\therefore DC\perp AC$. $\because AD$平分$\angle CAB,DE\perp AB,\therefore DC=DE$. 在$Rt\triangle ADC$和$Rt\triangle ADE$中，$\begin{cases}AD=AD,\\DC=DE,\end{cases}$ $\therefore Rt\triangle ADC\cong Rt\triangle ADE(HL).\therefore AC=AE$. $\because AC=BC,\angle C=90^{\circ},\therefore \angle B=\angle BAC=45^{\circ}$. $\because DE\perp AB,\therefore \angle B=\angle BDE=45^{\circ}.\therefore BE=DE$. $\therefore CD=DE=BE.\therefore AB=AE+BE=AC+CD$.