20. (13分)【发现问题】
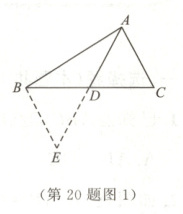
数学活动课上,王老师提出了如下问题:如图1,在$\triangle ABC$中,$AB = 5$,$AC = 3$,求$BC$边上的中线$AD$的取值范围.
【探究方法】
第一小组的同学经过合作交流,得到的解决方法如下:
①延长$AD$至点$E$,使$ED = AD$;
②连接$BE$,通过证明三角形全等把$AB$,$AC$,$2AD$转化到$\triangle ABE$中;
③利用三角形的三边关系可得$AE$的取值范围是$AB - BE < AE < AB + BE$,从而得到$AD$的取值范围.
【方法总结】
解题时,条件中若出现“中点”“中线”字样,可以考虑倍长中线构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形中.
(1)利用上述方法,请你直接写出$AD$的取值范围是
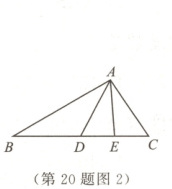
(2)如图2,$AD$是$\triangle ABC$的中线,$AE$是$\triangle ADC$的中线,$CA = CD$,$\angle CAD = \angle CDA$.下列结论:①$AB = 2AE$;②$\angle CAE = \angle DAE$;③$AE = AD$;④$\angle DAE = \angle DAB$.其中正确的是
【问题拓展】
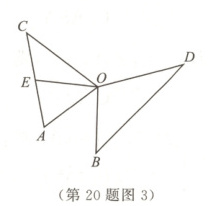
(3)如图3,$OA = OB$,$OC = OD$,$\angle AOB$与$\angle COD$互补,连接$AC$,$BD$,点$E$是$AC$的中点,连接$OE$.求证:$OE = \frac{1}{2}BD$.
【知识迁移】
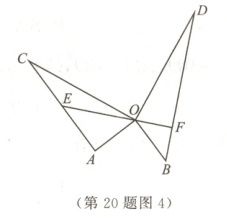
(4)如图4,在(3)的条件下,若$\angle AOB = 90°$,延长$EO$交$BD$于点$F$,$OF = 3$,$OE = 6$,求$\triangle AOC$的面积.
数学活动课上,王老师提出了如下问题:如图1,在$\triangle ABC$中,$AB = 5$,$AC = 3$,求$BC$边上的中线$AD$的取值范围.

【探究方法】
第一小组的同学经过合作交流,得到的解决方法如下:
①延长$AD$至点$E$,使$ED = AD$;
②连接$BE$,通过证明三角形全等把$AB$,$AC$,$2AD$转化到$\triangle ABE$中;
③利用三角形的三边关系可得$AE$的取值范围是$AB - BE < AE < AB + BE$,从而得到$AD$的取值范围.
【方法总结】
解题时,条件中若出现“中点”“中线”字样,可以考虑倍长中线构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形中.
(1)利用上述方法,请你直接写出$AD$的取值范围是
1<AD<4
.(2)如图2,$AD$是$\triangle ABC$的中线,$AE$是$\triangle ADC$的中线,$CA = CD$,$\angle CAD = \angle CDA$.下列结论:①$AB = 2AE$;②$\angle CAE = \angle DAE$;③$AE = AD$;④$\angle DAE = \angle DAB$.其中正确的是
①④
.(填序号)【问题拓展】
(3)如图3,$OA = OB$,$OC = OD$,$\angle AOB$与$\angle COD$互补,连接$AC$,$BD$,点$E$是$AC$的中点,连接$OE$.求证:$OE = \frac{1}{2}BD$.
【知识迁移】
(4)如图4,在(3)的条件下,若$\angle AOB = 90°$,延长$EO$交$BD$于点$F$,$OF = 3$,$OE = 6$,求$\triangle AOC$的面积.



答案:
(1)1<AD<4
【解析】易证△BDE≌△CDA(SAS).
∴BE=CA=3,ED=AD.
∴AE=2AD.
∵AB-BE<AE<AB+BE,
∴5-3<2AD<5+3,即1<AD<4.
(2)①④【解析】如图1,延长AE至点F,使FE=AE,连接DF.
易证△DEF≌△CEA(SAS).
∴∠EDF=∠C,DF=CA=CD=BD,∠DFE=∠CAE.
∴∠ADF=∠CDA+∠EDF=∠CAD+∠C.
∵∠ADB=∠CAD+∠C,
∴∠ADF=∠ADB.
易证△ADF≌△ADB(SAS).
∴AF=AB=2AE,∠DAE=∠DAB.
故①④正确,②③根据现有条件不能推出,故错误.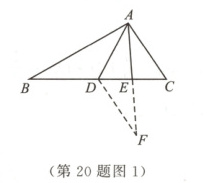
(3)证明:如图2,延长OE至点P,使EP=EO,连接AP.
∵点E是AC的中点,
∴AE=CE.
$\begin{cases}AE=CE,\\\angle AEP=\angle CEO,\\EP=EO,\end{cases}$
∴△AEP≌△CEO(SAS).
∴AP=CO=OD,∠EAP=∠C.
∴AP//CO.
∴∠AOC+∠OAP=180°.
∵∠AOB+∠COD=180°,
∴∠AOC+∠BOD=180°.
∴∠BOD=∠OAP.
$\begin{cases}OD=AP,\\\angle BOD=\angle OAP,\\OB=AO,\end{cases}$
∴△BOD≌△OAP(SAS).
∴BD=OP.
∵OE=$\frac{1}{2}$OP,
∴OE=$\frac{1}{2}$BD.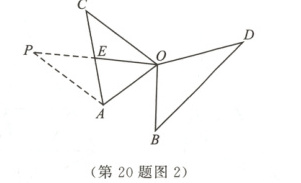
(4)解:如图3,延长OE至点P,使PE=OE,连接AP.
由
(3)得,△AEP≌△CEO,△BOD≌△OAP.
∴$S_{△AEP}=S_{△CEO},S_{△BOD}=S_{△OAP},\angle P=\angle COE=\angle D$.
∴$S_{△AOC}=S_{△AOE}+S_{△CEO}=S_{△AOE}+S_{△AEP}=S_{△OAP}=S_{△BOD}$.
∵∠AOB=90°,
∴∠COD=180°-∠AOB=90°.
∴∠COE+∠DOF=90°.
∴∠DOF+∠D=90°.
∴∠OFD=90°.
∵OE=6,
∴BD=2OE=12.
∵OF=3,
∴$S_{△AOC}=S_{△BOD}=\frac{1}{2}BD· OF=\frac{1}{2}×12×3=18$.
∴△AOC的面积是18.
(1)1<AD<4
【解析】易证△BDE≌△CDA(SAS).
∴BE=CA=3,ED=AD.
∴AE=2AD.
∵AB-BE<AE<AB+BE,
∴5-3<2AD<5+3,即1<AD<4.
(2)①④【解析】如图1,延长AE至点F,使FE=AE,连接DF.
易证△DEF≌△CEA(SAS).
∴∠EDF=∠C,DF=CA=CD=BD,∠DFE=∠CAE.
∴∠ADF=∠CDA+∠EDF=∠CAD+∠C.
∵∠ADB=∠CAD+∠C,
∴∠ADF=∠ADB.
易证△ADF≌△ADB(SAS).
∴AF=AB=2AE,∠DAE=∠DAB.
故①④正确,②③根据现有条件不能推出,故错误.

(3)证明:如图2,延长OE至点P,使EP=EO,连接AP.
∵点E是AC的中点,
∴AE=CE.
$\begin{cases}AE=CE,\\\angle AEP=\angle CEO,\\EP=EO,\end{cases}$
∴△AEP≌△CEO(SAS).
∴AP=CO=OD,∠EAP=∠C.
∴AP//CO.
∴∠AOC+∠OAP=180°.
∵∠AOB+∠COD=180°,
∴∠AOC+∠BOD=180°.
∴∠BOD=∠OAP.
$\begin{cases}OD=AP,\\\angle BOD=\angle OAP,\\OB=AO,\end{cases}$
∴△BOD≌△OAP(SAS).
∴BD=OP.
∵OE=$\frac{1}{2}$OP,
∴OE=$\frac{1}{2}$BD.

(4)解:如图3,延长OE至点P,使PE=OE,连接AP.
由
(3)得,△AEP≌△CEO,△BOD≌△OAP.
∴$S_{△AEP}=S_{△CEO},S_{△BOD}=S_{△OAP},\angle P=\angle COE=\angle D$.
∴$S_{△AOC}=S_{△AOE}+S_{△CEO}=S_{△AOE}+S_{△AEP}=S_{△OAP}=S_{△BOD}$.
∵∠AOB=90°,
∴∠COD=180°-∠AOB=90°.
∴∠COE+∠DOF=90°.
∴∠DOF+∠D=90°.
∴∠OFD=90°.
∵OE=6,
∴BD=2OE=12.
∵OF=3,
∴$S_{△AOC}=S_{△BOD}=\frac{1}{2}BD· OF=\frac{1}{2}×12×3=18$.
∴△AOC的面积是18.

查看更多完整答案,请扫码查看


