23. (13分)【探究发现】
(1)如图1,在△ABC中,AB = AC,∠BAC = 90°,点D为BC的中点,点E,F分别是边AC,AB上的点. 若∠EDF = 90°,则AE,AF,AB之间的数量关系是
【类比应用】
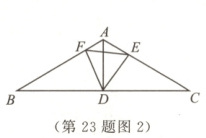
(2)如图2,在△ABC中,AB = AC,∠BAC = 120°,点D是BC的中点,点E,F分别是边AC,AB上的点. 若∠EDF = 60°,试探究AE,AF,AB之间的数量关系,并说明理由.
【拓展延伸】
(3)在△ABC中,AB = AC = 5,∠BAC = 120°,点D是BC的中点,点E,F分别是直线AC,AB上的点. 若CE = 1,∠EDF = 60°,连接EF,请直接写出AF的长.
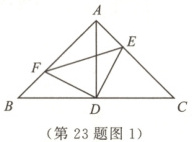
(1)如图1,在△ABC中,AB = AC,∠BAC = 90°,点D为BC的中点,点E,F分别是边AC,AB上的点. 若∠EDF = 90°,则AE,AF,AB之间的数量关系是
$AE + AF = AB$
.【类比应用】
(2)如图2,在△ABC中,AB = AC,∠BAC = 120°,点D是BC的中点,点E,F分别是边AC,AB上的点. 若∠EDF = 60°,试探究AE,AF,AB之间的数量关系,并说明理由.
【拓展延伸】
(3)在△ABC中,AB = AC = 5,∠BAC = 120°,点D是BC的中点,点E,F分别是直线AC,AB上的点. 若CE = 1,∠EDF = 60°,连接EF,请直接写出AF的长.



答案:
23.
(1)$AE + AF = AB$
(2)$AE + AF = \frac{1}{2}AB$.
理由:如图1,取AB的中点G,连接DG.
$\because AB = AC$,$\angle BAC = 120^{\circ}$,点D是AC的中点,
$\therefore \angle B = \angle C = 30^{\circ}$,$\angle BAD = \angle CAD = 60^{\circ}$.
在$Rt \triangle ABD$中,$\because \angle B = 30^{\circ}$,$\therefore AB = 2AD$.
$\because$点G是AB的中点,$\therefore AG = BG = AD$.
$\because \angle DAG = 60^{\circ}$,$\therefore \triangle AGD$是等边三角形.
$\therefore DG = DA$,$\angle DGA = \angle ADG = 60^{\circ}$.
$\therefore \angle DAE = \angle DGF$.
$\because \angle EDF = 60^{\circ}$,$\therefore \angle EDA + \angle FDA = 60^{\circ}$.
$\because \angle FDG + \angle FDA = 60^{\circ}$,$\therefore \angle EDA = \angle FDG$.
在$\triangle DAE$和$\triangle DGF$中,$\begin{cases} \angle EDA = \angle FDG, \\ DA = DG, \\ \angle DAE = \angle DGF, \end{cases}$
$\therefore \triangle DAE \cong \triangle DGF (ASA)$.$\therefore AE = GF$.
$\therefore AE + AF = GF + AF = AG = \frac{1}{2}AB$.
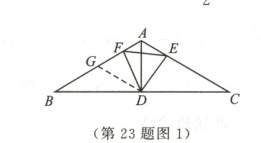
(3)AF的长是1.5或3.5.
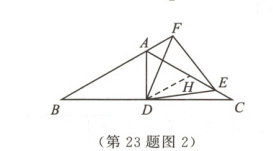
[解析]Ⅰ.如图2,当点E在线段AC上时,点F在BA的延长线上,取AC的中点H,连接DH.
易证$\triangle ADH$是等边三角形.
$\therefore \angle DHE = \angle DAF = 180^{\circ} - 60^{\circ} = 120^{\circ}$.
易证$\triangle DAF \cong \triangle DHE (ASA)$.
$\therefore AF = HE = HC - CE = \frac{1}{2}AC - CE = 1.5$.
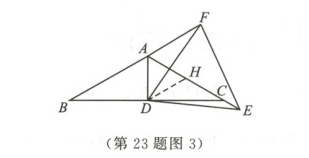
Ⅱ.如图3,当点E在AC的延长线上时,点F在BA的延长线上,取AC的中点H,连接DH.
同理可证$\triangle ADF \cong \triangle HDE (ASA)$.
$\therefore AF = HE = HC + CE = \frac{1}{2}AC + CE = 3.5$.
综上所述,AF的长是1.5或3.5.
23.
(1)$AE + AF = AB$
(2)$AE + AF = \frac{1}{2}AB$.
理由:如图1,取AB的中点G,连接DG.
$\because AB = AC$,$\angle BAC = 120^{\circ}$,点D是AC的中点,
$\therefore \angle B = \angle C = 30^{\circ}$,$\angle BAD = \angle CAD = 60^{\circ}$.
在$Rt \triangle ABD$中,$\because \angle B = 30^{\circ}$,$\therefore AB = 2AD$.
$\because$点G是AB的中点,$\therefore AG = BG = AD$.
$\because \angle DAG = 60^{\circ}$,$\therefore \triangle AGD$是等边三角形.
$\therefore DG = DA$,$\angle DGA = \angle ADG = 60^{\circ}$.
$\therefore \angle DAE = \angle DGF$.
$\because \angle EDF = 60^{\circ}$,$\therefore \angle EDA + \angle FDA = 60^{\circ}$.
$\because \angle FDG + \angle FDA = 60^{\circ}$,$\therefore \angle EDA = \angle FDG$.
在$\triangle DAE$和$\triangle DGF$中,$\begin{cases} \angle EDA = \angle FDG, \\ DA = DG, \\ \angle DAE = \angle DGF, \end{cases}$
$\therefore \triangle DAE \cong \triangle DGF (ASA)$.$\therefore AE = GF$.
$\therefore AE + AF = GF + AF = AG = \frac{1}{2}AB$.

(3)AF的长是1.5或3.5.
[解析]Ⅰ.如图2,当点E在线段AC上时,点F在BA的延长线上,取AC的中点H,连接DH.
易证$\triangle ADH$是等边三角形.
$\therefore \angle DHE = \angle DAF = 180^{\circ} - 60^{\circ} = 120^{\circ}$.
易证$\triangle DAF \cong \triangle DHE (ASA)$.
$\therefore AF = HE = HC - CE = \frac{1}{2}AC - CE = 1.5$.

Ⅱ.如图3,当点E在AC的延长线上时,点F在BA的延长线上,取AC的中点H,连接DH.
同理可证$\triangle ADF \cong \triangle HDE (ASA)$.
$\therefore AF = HE = HC + CE = \frac{1}{2}AC + CE = 3.5$.

综上所述,AF的长是1.5或3.5.
查看更多完整答案,请扫码查看


