23.(13分)已知点$A(0,6)$,$B(-6,0)$,将线段$OA$绕点$O$顺时针旋转至$OC$,连接$AC$,$BC$.
(1)如图1,求$\angle ACB$的度数.
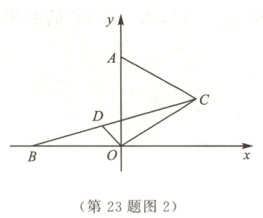
(2)如图2,若$\angle AOC = 60^{\circ}$,$\angle AOB$的平分线$OD$交$BC$于点$D$,求证:$OD + BD = CD$.
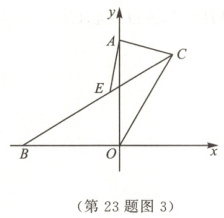
(3)如图3,若$\angle AOC = 30^{\circ}$,过点$A$作$AE\bot AC$交$BC$于点$E$,求$BE$的长.
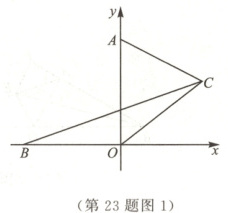
(1)如图1,求$\angle ACB$的度数.
(2)如图2,若$\angle AOC = 60^{\circ}$,$\angle AOB$的平分线$OD$交$BC$于点$D$,求证:$OD + BD = CD$.
(3)如图3,若$\angle AOC = 30^{\circ}$,过点$A$作$AE\bot AC$交$BC$于点$E$,求$BE$的长.



答案:
23.
(1)解:$\because$点$A(0,6)$,$B(-6,0)$,$\therefore OA=OB=6$. 由旋转得,$OC=OA$,$\therefore OC=OB=OA$. 设$\angle AOC=2\alpha$,$\therefore \angle BOC=\angle AOB+\angle AOC=90^{\circ}+2\alpha$. $\therefore \angle OBC=\angle OCB=\frac{1}{2}(180^{\circ}-\angle BOC)=45^{\circ}-\alpha$. $\because \angle AOC=2\alpha$,$\therefore \angle OAC=\angle OCA=90^{\circ}-\alpha$. $\therefore \angle ACB=\angle OCA-\angle OCB=90^{\circ}-\alpha-(45^{\circ}-\alpha)=45^{\circ}$.
(2)证明:如图1,在$BC$上取点$H$,使$CH=BD$. 在$\triangle BOD$和$\triangle COH$中,$\begin{cases}BO=CO,\\\angle OBD=\angle OCH,\\BD=CH,\end{cases}$ $\therefore \triangle BOD\cong\triangle COH(SAS)$. $\therefore \angle BOD=\angle COH$,$OD=OH$. $\because OD$平分$\angle AOB$,$\therefore \angle BOD=\angle AOD=45^{\circ}$. $\therefore \angle COH=\angle BOD=45^{\circ}$. $\because \angle BOC=\angle AOC+\angle AOB=60^{\circ}+90^{\circ}=150^{\circ}$, $\therefore \angle DOH=\angle BOC-\angle BOD-\angle COH=60^{\circ}$. $\therefore \triangle DOH$为等边三角形,$\therefore OD=DH$. $\therefore OD+BD=DH+BD=DH+HC=CD$.
(3)解:如图2,过点$C$作$CN\perp AO$于点$N$,过点$E$作$EM\perp AO$于点$M$,连接$OE$. $\therefore \angle CNA=\angle AME=90^{\circ}$. 由
(1)得,$\angle ACE=45^{\circ}$. $\because AE\perp AC$,$\therefore \angle CAE=90^{\circ}$. $\therefore \angle AEC=90^{\circ}-\angle ACE=45^{\circ}$. $\therefore \angle ACE=\angle AEC$,$\therefore AC=AE$. $\because \angle ACN+\angle NAC=\angle EAM+\angle NAC=90^{\circ}$, $\therefore \angle ACN=\angle EAM$. 在$\triangle AEM$和$\triangle CAN$中,$\begin{cases}\angle AME=\angle CNA,\\\angle EAM=\angle ACN,\\AE=CA,\end{cases}$ $\therefore \triangle AEM\cong\triangle CAN(AAS)$,$\therefore AM=CN$. 在$Rt\triangle CNO$中,$\angle CNO=90^{\circ}$,$\angle AOC=30^{\circ}$,$OB=OA=OC=6$,$\therefore CN=\frac{1}{2}CO=3$. $\therefore AM=3$,$\therefore OM=OA - AM=3$,$\therefore OM=AM$. $\because EM\perp AO$,$\therefore AE=EO$. $\because \angle AOB=90^{\circ}$,$\angle AOC=30^{\circ}$, $\therefore \angle BOC=\angle AOB+\angle AOC=120^{\circ}$. $\therefore \angle CBO=\angle OCB=30^{\circ}$,$\therefore \angle OAC=\angle OCA=75^{\circ}$. $\therefore \angle EAO=\angle EOA=\angle CAE-\angle OAC=90^{\circ}-75^{\circ}=15^{\circ}$. $\therefore \angle BOE=\angle AOB-\angle EOA=75^{\circ}$. $\therefore \angle BEO=180^{\circ}-\angle CBO-\angle BOE=75^{\circ}$. $\therefore \angle BOE=\angle BEO$,$\therefore BE=BO=6$.
(1)解:$\because$点$A(0,6)$,$B(-6,0)$,$\therefore OA=OB=6$. 由旋转得,$OC=OA$,$\therefore OC=OB=OA$. 设$\angle AOC=2\alpha$,$\therefore \angle BOC=\angle AOB+\angle AOC=90^{\circ}+2\alpha$. $\therefore \angle OBC=\angle OCB=\frac{1}{2}(180^{\circ}-\angle BOC)=45^{\circ}-\alpha$. $\because \angle AOC=2\alpha$,$\therefore \angle OAC=\angle OCA=90^{\circ}-\alpha$. $\therefore \angle ACB=\angle OCA-\angle OCB=90^{\circ}-\alpha-(45^{\circ}-\alpha)=45^{\circ}$.
(2)证明:如图1,在$BC$上取点$H$,使$CH=BD$. 在$\triangle BOD$和$\triangle COH$中,$\begin{cases}BO=CO,\\\angle OBD=\angle OCH,\\BD=CH,\end{cases}$ $\therefore \triangle BOD\cong\triangle COH(SAS)$. $\therefore \angle BOD=\angle COH$,$OD=OH$. $\because OD$平分$\angle AOB$,$\therefore \angle BOD=\angle AOD=45^{\circ}$. $\therefore \angle COH=\angle BOD=45^{\circ}$. $\because \angle BOC=\angle AOC+\angle AOB=60^{\circ}+90^{\circ}=150^{\circ}$, $\therefore \angle DOH=\angle BOC-\angle BOD-\angle COH=60^{\circ}$. $\therefore \triangle DOH$为等边三角形,$\therefore OD=DH$. $\therefore OD+BD=DH+BD=DH+HC=CD$.
(3)解:如图2,过点$C$作$CN\perp AO$于点$N$,过点$E$作$EM\perp AO$于点$M$,连接$OE$. $\therefore \angle CNA=\angle AME=90^{\circ}$. 由
(1)得,$\angle ACE=45^{\circ}$. $\because AE\perp AC$,$\therefore \angle CAE=90^{\circ}$. $\therefore \angle AEC=90^{\circ}-\angle ACE=45^{\circ}$. $\therefore \angle ACE=\angle AEC$,$\therefore AC=AE$. $\because \angle ACN+\angle NAC=\angle EAM+\angle NAC=90^{\circ}$, $\therefore \angle ACN=\angle EAM$. 在$\triangle AEM$和$\triangle CAN$中,$\begin{cases}\angle AME=\angle CNA,\\\angle EAM=\angle ACN,\\AE=CA,\end{cases}$ $\therefore \triangle AEM\cong\triangle CAN(AAS)$,$\therefore AM=CN$. 在$Rt\triangle CNO$中,$\angle CNO=90^{\circ}$,$\angle AOC=30^{\circ}$,$OB=OA=OC=6$,$\therefore CN=\frac{1}{2}CO=3$. $\therefore AM=3$,$\therefore OM=OA - AM=3$,$\therefore OM=AM$. $\because EM\perp AO$,$\therefore AE=EO$. $\because \angle AOB=90^{\circ}$,$\angle AOC=30^{\circ}$, $\therefore \angle BOC=\angle AOB+\angle AOC=120^{\circ}$. $\therefore \angle CBO=\angle OCB=30^{\circ}$,$\therefore \angle OAC=\angle OCA=75^{\circ}$. $\therefore \angle EAO=\angle EOA=\angle CAE-\angle OAC=90^{\circ}-75^{\circ}=15^{\circ}$. $\therefore \angle BOE=\angle AOB-\angle EOA=75^{\circ}$. $\therefore \angle BEO=180^{\circ}-\angle CBO-\angle BOE=75^{\circ}$. $\therefore \angle BOE=\angle BEO$,$\therefore BE=BO=6$.
查看更多完整答案,请扫码查看


