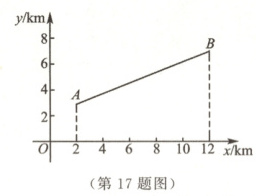
17. (10分)某乡为了解决干旱问题,要在某河道上建一座水泵站,分别向河同一侧的张村A和李村B送水. 经实地勘查后,工程人员设计图纸时,以河道上大桥的位置点O为坐标原点,以河道所在的直线为x轴建立如图所示的平面直角坐标系,两村的坐标分别是点A(2,3),B(12,7).
(1)若从节约经费的角度考虑,水泵站建在何处可以使所用输水管最短?(保留作图痕迹,不写作法)
(2)当水泵站建在距离点O
(1)若从节约经费的角度考虑,水泵站建在何处可以使所用输水管最短?(保留作图痕迹,不写作法)
(2)当水泵站建在距离点O
9
km的点D处时,可使它到张村A和李村B的距离相等.(在图中标出点D的位置并填空)
答案:
1. (1)
作点$A$关于$x$轴的对称点$A'$,连接$A'B$与$x$轴的交点$P$,则点$P$即为所求水泵站的位置(作图痕迹略)。
理由:根据轴对称的性质,$AP = A'P$,所以$AP + BP=A'P + BP$。根据两点之间线段最短,$A'$,$P$,$B$三点共线时,$A'P + BP$最短,即$AP + BP$最短。
2. (2)
设$D(x,0)$,已知$A(2,3)$,$B(12,7)$,由$AD = BD$,根据两点间距离公式$d=\sqrt{(x_2 - x_1)^2+(y_2 - y_1)^2}$,可得:
$\sqrt{(x - 2)^2+3^2}=\sqrt{(x - 12)^2+7^2}$。
两边平方得$(x - 2)^2+9=(x - 12)^2+49$。
展开式子:$x^{2}-4x + 4+9=x^{2}-24x + 144+49$。
移项:$x^{2}-4x - x^{2}+24x=144 + 49-4 - 9$。
合并同类项:$20x=180$。
解得$x = 9$,所以$D(9,0)$。
故答案为$9$。
作点$A$关于$x$轴的对称点$A'$,连接$A'B$与$x$轴的交点$P$,则点$P$即为所求水泵站的位置(作图痕迹略)。
理由:根据轴对称的性质,$AP = A'P$,所以$AP + BP=A'P + BP$。根据两点之间线段最短,$A'$,$P$,$B$三点共线时,$A'P + BP$最短,即$AP + BP$最短。
2. (2)
设$D(x,0)$,已知$A(2,3)$,$B(12,7)$,由$AD = BD$,根据两点间距离公式$d=\sqrt{(x_2 - x_1)^2+(y_2 - y_1)^2}$,可得:
$\sqrt{(x - 2)^2+3^2}=\sqrt{(x - 12)^2+7^2}$。
两边平方得$(x - 2)^2+9=(x - 12)^2+49$。
展开式子:$x^{2}-4x + 4+9=x^{2}-24x + 144+49$。
移项:$x^{2}-4x - x^{2}+24x=144 + 49-4 - 9$。
合并同类项:$20x=180$。
解得$x = 9$,所以$D(9,0)$。
故答案为$9$。
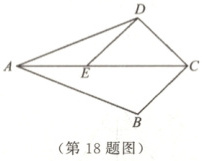
18. (10分)如图,已知AC平分∠BAD,连接CB,CD,过点D作DE//BC交AC于点E,DE = DC. 求证:AD = AB.

答案:
18.证明:
∵DE=DC,
∴∠DEC=∠DCA.
∵DE//BC,
∴∠DEC=∠BCA.
∴∠DCA=∠BCA.
∵AC平分∠BAD,
∴∠DAC=∠BAC.
在△ACD和△ACB中,
∠DCA=∠BCA,
AC=AC,
∠DAC=∠BAC,
∴△ACD≌△ACB(ASA).
∴AD=AB.
∵DE=DC,
∴∠DEC=∠DCA.
∵DE//BC,
∴∠DEC=∠BCA.
∴∠DCA=∠BCA.
∵AC平分∠BAD,
∴∠DAC=∠BAC.
在△ACD和△ACB中,
∠DCA=∠BCA,
AC=AC,
∠DAC=∠BAC,
∴△ACD≌△ACB(ASA).
∴AD=AB.
查看更多完整答案,请扫码查看


