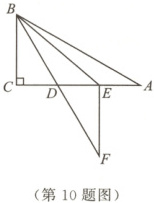
10. ◆2025·大连沙河口区期末◆ 如图,在△ABC中,$ \angle C = 90°$,$ \angle A = 30°$,BD平分$ \angle ABC$,点E是AD的中点,过点E作AC的垂线,与BD的延长线交于点F.下列结论:①BC = EF;②DF = 2CD;③$ \angle CEB = 45°$;④$S_{\triangle BEF} = 2S_{\triangle BEA}$.其中正确的有 (
A.1个
B.2个
C.3个
D.4个
C
)
A.1个
B.2个
C.3个
D.4个
答案:
10.C
11. 若等腰三角形的顶角是110°,则腰上的高与底边的夹角的度数是
$55^{\circ}$
.
答案:
11.$55^{\circ}$
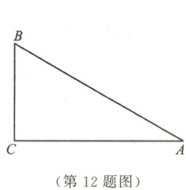
12. 如图,在Rt△ABC中,$ \angle C = 90°$,$ \angle A = 30°$.若AB + BC = 12cm,则AB的长是
8
cm.
答案:
12.8
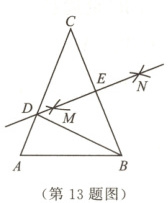
13. ◆2025·沈阳沈河区期末◆ 如图,在△ABC中,AC = BC = 8,AB = 6,分别以点B和点C为圆心,大于$ \frac{1}{2}BC$的长为半径作弧,两弧相交于点M,N,作直线MN,分别交AC,BC于点D,E,连接BD,则△ABD的周长为
14
.
答案:
13.14
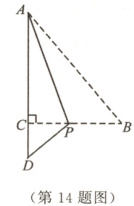
14. 如图,在三角形纸片ABC中,$ \angle ACB = 90°$,在BC边上取一点P,将△ABC沿AP折叠,使点B与AC延长线上的点D重合.若$ \angle CPD = 40°$,则$ \angle PAC$的度数是
$20^{\circ}$
.
答案:
14.$20^{\circ}$
15. 如图,在△ABC中,AB = AC = 5,$S_{\triangle ABC} = 12$,AD是△ABC的中线,点F是线段AD上的动点,点E是AC边上的动点,连接EF,CF,则CF + EF的最小值是
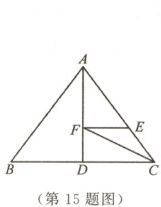
$\frac{24}{5}$
.
答案:
15.$\frac{24}{5}$ 【解析】连接$BF$.易证$BF=CF$.
$\therefore CF+EF=BF+EF$.
$\therefore$当点$B$,$F$,$E$共线且$BE\perp AC$时,$CF+EF$的值最小.此时$BE=CF+EF$.
$\because AC=5$,$\therefore S_{\triangle ABC}=\frac{1}{2}BE· AC=12.\therefore BE=\frac{24}{5}$.
$\therefore CF+EF$的最小值是$\frac{24}{5}$.
$\therefore CF+EF=BF+EF$.
$\therefore$当点$B$,$F$,$E$共线且$BE\perp AC$时,$CF+EF$的值最小.此时$BE=CF+EF$.
$\because AC=5$,$\therefore S_{\triangle ABC}=\frac{1}{2}BE· AC=12.\therefore BE=\frac{24}{5}$.
$\therefore CF+EF$的最小值是$\frac{24}{5}$.
16. (10分)如图,在△ABC中,AB = AC,点D,E在边BC上,且BD = CE.求证:$ \angle ADE = \angle AED$.
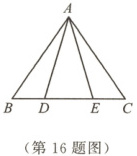

答案:
16.证明:$\because AB=AC$,$\therefore \angle B=\angle C$.
在$\triangle ABD$和$\triangle ACE$中,$\begin{cases}AB=AC,\\\angle B=\angle C,\\BD=CE,\end{cases}$
$\therefore \triangle ABD\cong\triangle ACE(SAS)$.
$\therefore AD=AE.\therefore \angle ADE=\angle AED$.
在$\triangle ABD$和$\triangle ACE$中,$\begin{cases}AB=AC,\\\angle B=\angle C,\\BD=CE,\end{cases}$
$\therefore \triangle ABD\cong\triangle ACE(SAS)$.
$\therefore AD=AE.\therefore \angle ADE=\angle AED$.
查看更多完整答案,请扫码查看


