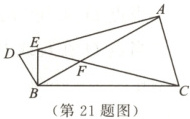
21. (8分)如图,在等腰三角形ABC中,AB = CB,点F在AB边上,连接CF并延长,交AD于点E,BD = BE,∠DBE = ∠ABC.
(1)求证:AD = CE.
(2)若∠ABC = 30°,∠AFC = 45°,求∠EAC的度数.
(1)求证:AD = CE.
(2)若∠ABC = 30°,∠AFC = 45°,求∠EAC的度数.

答案:
21.
(1)证明:$\because \angle DBE = \angle ABC$,
$\therefore \angle DBE + \angle ABE = \angle ABC + \angle ABE$,
即$\angle ABD = \angle CBE$.
在$\triangle ADB$和$\triangle CEB$中,$\begin{cases} AB = CB, \\ \angle ABD = \angle CBE, \\ BD = BE, \end{cases}$
$\therefore \triangle ADB \cong \triangle CEB (SAS)$.$\therefore AD = CE$.
(2)解:$\because BA = BC$,$\angle ABC = 30^{\circ}$,
$\therefore \angle BAC = \angle BCA = \frac{1}{2}(180^{\circ} - \angle ABC) = 75^{\circ}$.
$\because \angle AFC = 45^{\circ}$,$\therefore \angle BCE = \angle AFC - \angle ABC = 15^{\circ}$.
由
(1)得$\triangle ADB \cong \triangle CEB$,$\therefore \angle BAD = \angle BCE = 15^{\circ}$.
$\therefore \angle EAC = \angle BAD + \angle BAC = 90^{\circ}$.
(1)证明:$\because \angle DBE = \angle ABC$,
$\therefore \angle DBE + \angle ABE = \angle ABC + \angle ABE$,
即$\angle ABD = \angle CBE$.
在$\triangle ADB$和$\triangle CEB$中,$\begin{cases} AB = CB, \\ \angle ABD = \angle CBE, \\ BD = BE, \end{cases}$
$\therefore \triangle ADB \cong \triangle CEB (SAS)$.$\therefore AD = CE$.
(2)解:$\because BA = BC$,$\angle ABC = 30^{\circ}$,
$\therefore \angle BAC = \angle BCA = \frac{1}{2}(180^{\circ} - \angle ABC) = 75^{\circ}$.
$\because \angle AFC = 45^{\circ}$,$\therefore \angle BCE = \angle AFC - \angle ABC = 15^{\circ}$.
由
(1)得$\triangle ADB \cong \triangle CEB$,$\therefore \angle BAD = \angle BCE = 15^{\circ}$.
$\therefore \angle EAC = \angle BAD + \angle BAC = 90^{\circ}$.
查看更多完整答案,请扫码查看


