19.(12分)探索发现:$\frac{1}{1 × 2}=1-\frac{1}{2}$,$\frac{1}{2 × 3}=\frac{1}{2}-\frac{1}{3}$,$\frac{1}{3 × 4}=\frac{1}{3}-\frac{1}{4}$,……
根据你发现的规律,解答下列问题:
(1)$\frac{1}{4 × 5}=$
(2)利用你发现的规律计算:$\frac{1}{1 × 2}+\frac{1}{2 × 3}+\frac{1}{3 × 4}+ ·s +\frac{1}{n(n+1)}$($n$为正整数,$n>4$)
(3)探索规律并解方程:$\frac{1}{x(x+2)}+\frac{1}{(x+2)(x+4)}+ ·s +\frac{1}{(x+98)(x+100)}=\frac{1}{x+100}$
根据你发现的规律,解答下列问题:
(1)$\frac{1}{4 × 5}=$
$\frac{1}{4}$−$\frac{1}{5}$
,$\frac{1}{n(n+1)}=$$\frac{1}{n}-\frac{1}{n + 1}$
($n$为正整数)(2)利用你发现的规律计算:$\frac{1}{1 × 2}+\frac{1}{2 × 3}+\frac{1}{3 × 4}+ ·s +\frac{1}{n(n+1)}$($n$为正整数,$n>4$)
(3)探索规律并解方程:$\frac{1}{x(x+2)}+\frac{1}{(x+2)(x+4)}+ ·s +\frac{1}{(x+98)(x+100)}=\frac{1}{x+100}$
答案:
19.
(1)$\frac{1}{4}$−$\frac{1}{5}$
(2)解:$\frac{1}{1×2}+\frac{1}{2×3}+\frac{1}{3×4}+·s+\frac{1}{n(n+1)}$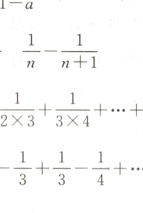
=$1−\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+·s+\frac{1}{n}−\frac{1}{n+1}$
=$1−\frac{1}{n+1}$
=$\frac{n}{n+1}$.
(3)解:
∵$\frac{1}{x(x+2)}+\frac{1}{(x+2)(x+4)}+·s+\frac{1}{(x+98)(x+100)}=\frac{1}{x+100}$
∴$\frac{1}{2}(\frac{1}{x}-\frac{1}{x+2})+\frac{1}{2}(\frac{1}{x+2}-\frac{1}{x+4})+·s+\frac{1}{2}(\frac{1}{x+98}-\frac{1}{x+100})=\frac{1}{x+100}$
∴$\frac{1}{2}(\frac{1}{x}-\frac{1}{x+100})=\frac{1}{x+100}$
∴$\frac{1}{x}=\frac{3}{x+100}$,解得$x=50$.
检验:当$x=50$时,$x,x+2,x+4,·s,x+100\neq0$.
∴原分式方程的解是$x=50$.
19.
(1)$\frac{1}{4}$−$\frac{1}{5}$
(2)解:$\frac{1}{1×2}+\frac{1}{2×3}+\frac{1}{3×4}+·s+\frac{1}{n(n+1)}$
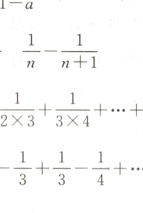
=$1−\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+·s+\frac{1}{n}−\frac{1}{n+1}$
=$1−\frac{1}{n+1}$
=$\frac{n}{n+1}$.
(3)解:
∵$\frac{1}{x(x+2)}+\frac{1}{(x+2)(x+4)}+·s+\frac{1}{(x+98)(x+100)}=\frac{1}{x+100}$
∴$\frac{1}{2}(\frac{1}{x}-\frac{1}{x+2})+\frac{1}{2}(\frac{1}{x+2}-\frac{1}{x+4})+·s+\frac{1}{2}(\frac{1}{x+98}-\frac{1}{x+100})=\frac{1}{x+100}$
∴$\frac{1}{2}(\frac{1}{x}-\frac{1}{x+100})=\frac{1}{x+100}$
∴$\frac{1}{x}=\frac{3}{x+100}$,解得$x=50$.
检验:当$x=50$时,$x,x+2,x+4,·s,x+100\neq0$.
∴原分式方程的解是$x=50$.
20.(13分) ◆2025·玉林期末◆ 某中学为了践行劳动课程标准和让学生体验农耕劳动,开辟了一处耕种园,需要采购一批菜苗开展种植活动.据调查:每捆A种菜苗,在市场上购买的价格是在菜苗基地处购买的1.5倍,用900元在市场上购买的A种菜苗数量比在菜苗基地处购买数量的一半要多5捆.
(1)求菜苗基地每捆A种菜苗的价格.
(2)菜苗基地每捆B种菜苗的价格是35元,学校预计用不多于2140元的资金在菜苗基地购买A,B两种菜苗共80捆,同时菜苗基地为支持该校活动,对A,B两种菜苗均提供八折优惠.求至少可购买多少捆A种菜苗.
(1)求菜苗基地每捆A种菜苗的价格.
(2)菜苗基地每捆B种菜苗的价格是35元,学校预计用不多于2140元的资金在菜苗基地购买A,B两种菜苗共80捆,同时菜苗基地为支持该校活动,对A,B两种菜苗均提供八折优惠.求至少可购买多少捆A种菜苗.
答案:
20.解:
(1)设菜苗基地每捆A种菜苗的价格是$x$元,则在市场上购买每捆A种菜苗的价格是$1.5x$元.由题意得,$\frac{1}{2}×\frac{900}{x}+5=\frac{900}{1.5x}$.解得$x=30$.
经检验,$x=30$是原方程的解,且符合题意.
答:菜苗基地每捆A种菜苗的价格是30元.
(2)设在菜苗基地购买$m$捆A种菜苗,则在菜苗基地购买$(80 - m)$捆B种菜苗.
由题意得$30×0.8m+35×0.8(80 - m)\leq2140$ .解得$m\geq25$.
.解得$m\geq25$.
答:至少可购买25捆A种菜苗.
20.解:
(1)设菜苗基地每捆A种菜苗的价格是$x$元,则在市场上购买每捆A种菜苗的价格是$1.5x$元.由题意得,$\frac{1}{2}×\frac{900}{x}+5=\frac{900}{1.5x}$.解得$x=30$.
经检验,$x=30$是原方程的解,且符合题意.
答:菜苗基地每捆A种菜苗的价格是30元.
(2)设在菜苗基地购买$m$捆A种菜苗,则在菜苗基地购买$(80 - m)$捆B种菜苗.
由题意得$30×0.8m+35×0.8(80 - m)\leq2140$
 .解得$m\geq25$.
.解得$m\geq25$.答:至少可购买25捆A种菜苗.
查看更多完整答案,请扫码查看


