8. 如图,四边形$ABCD$的对角线$AC$,$BD$相交于点$O$,$\triangle ABO \cong \triangle ADO$.下列结论:①$AC \perp BD$;②$CB = CD$;③$DA = DC$;④$\triangle ABC \cong \triangle ADC$.其中正确的是 (
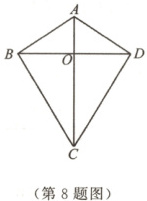
A.①②
B.②④
C.②③
D.①②④
D
)
A.①②
B.②④
C.②③
D.①②④
答案:
8.D
9. 如图,$BP$平分$\angle ABC$,点$D$是$BP$上一点,点$E$,$F$分别在$BA$,$BC$上,且满足$DE = DF$,$BE \neq BF$.若$\angle BED = 140°$,则$\angle BFD$的度数是 (
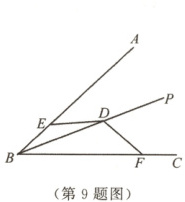
A.$40°$
B.$50°$
C.$60°$
D.$70°$
A
)
A.$40°$
B.$50°$
C.$60°$
D.$70°$
答案:
9.A
10. ◆2024·本溪期末◆ 如图,在$\triangle ABC$中,$\angle C = 90°$,以点$A$为圆心,适当长为半径作弧,分别交$AB$,$AC$于点$M$,$N$,再分别以点$M$,$N$为圆心,大于$\frac{1}{2}MN$的长为半径作弧,两弧相交于点$G$,作射线$AG$交$BC$于点$D$.若$BD = 5$,$CD = 3$,点$P$是边$AB$上一动点,则$PD$的最小值是 (
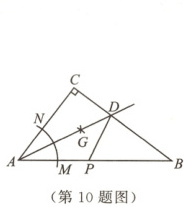
A.2
B.3
C.5
D.8
B
)
A.2
B.3
C.5
D.8
答案:
10.B
11. 如图,若$\triangle ABC \cong \triangle CDA$,则$AB$与$CD$之间的位置关系是
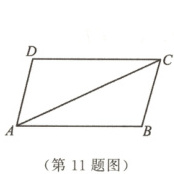
AB//CD
.
答案:
11.AB//CD
12. 如图,点$B$是$AD$的中点,点$C$,$E$为$AD$右侧两点,连接$AC$,$BC$,$BE$,$DE$,$AC = DE$.请添加一个条件,使得$\triangle ABC \cong \triangle DBE$,可以添加的条件是

BC=BE
.(写出一个即可)
答案:
12.答案不唯一,如:BC=BE
13. 如图,在$\triangle ABC$中,$CD$是$AB$边上的高,$BE$平分$\angle ABC$交$CD$于点$E$.若$BC = 6$,$DE = 3$,则$\triangle BCE$的面积是
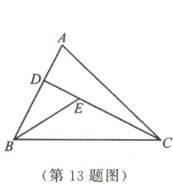
9
.
答案:
13.9
14. 如图,在$\triangle ABC$中,点$D$,$E$,$F$分别是$BC$,$AC$,$AB$上的点,且$BF = CD$,$BD = CE$.若$\angle A = 56°$,$\angle C = 62°$,则$\angle EDF$的度数是
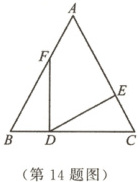
62°
.
答案:
14.62°【解析】
∵∠A=56°,∠C=62°,
∴∠B=180°-∠A-∠C=62°.
易证△FBD≌△DCE(SAS).
∴∠BFD=∠CDE.
∵∠FDC=∠EDF+∠CDE,
∠FDC=∠B+∠BFD,
∴∠EDF=∠B=62°.
∵∠A=56°,∠C=62°,
∴∠B=180°-∠A-∠C=62°.
易证△FBD≌△DCE(SAS).
∴∠BFD=∠CDE.
∵∠FDC=∠EDF+∠CDE,
∠FDC=∠B+∠BFD,
∴∠EDF=∠B=62°.
15. 如图,在$ Rt \triangle ABC$中,$\angle ACB = 90°$,$AC = BC$,$AB = 6$,动点$P$从点$A$出发,以每秒2个单位长度的速度在射线$AB$上运动,连接$CP$,以$CP$为直角边向右作$ Rt \triangle CDP$,使$\angle DCP = 90°$,$CP = CD$,连接$BD$.设点$P$的运动时间是$t$秒,当$BD = 2BP$时,$t$的值是
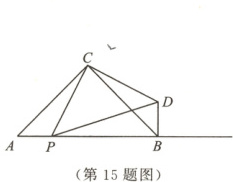
2或6
.
答案:
15.2或6【解析】
∵CA=CB,CP=CD,∠ACB=∠PCD=90°,
易证△CAP≌△CBD(SAS).
∴AP=BD=2t.
若BD=2BP,则AP=2BP.
当0<t≤3时,2t=2(6 - 2t),解得t=2.
当t>3时,2t=2(2t - 6),解得t=6.
综上所述,t的值是2或6.
∵CA=CB,CP=CD,∠ACB=∠PCD=90°,
易证△CAP≌△CBD(SAS).
∴AP=BD=2t.
若BD=2BP,则AP=2BP.
当0<t≤3时,2t=2(6 - 2t),解得t=2.
当t>3时,2t=2(2t - 6),解得t=6.
综上所述,t的值是2或6.
查看更多完整答案,请扫码查看


