9. 新情境 数学文化 中世纪意大利数学家斐波那契编写的《计算之书》记载了一道数学题,其大意是:一组人平分90枚硬币,每人分得若干,若再加上6人,平分120枚硬币,则第二次每人所得的硬币数与第一次相同.求第二次分硬币的人数.设第一次分硬币的人数是$x$人,则可列方程为(
A.$90x = 120(x + 6)$
B.$\frac{90}{x - 6} = \frac{120}{x}$
C.$90(x - 6) = 120x$
D.$\frac{90}{x} = \frac{120}{x + 6}$
D
)A.$90x = 120(x + 6)$
B.$\frac{90}{x - 6} = \frac{120}{x}$
C.$90(x - 6) = 120x$
D.$\frac{90}{x} = \frac{120}{x + 6}$
答案:
9.D
10. 如图,在$\triangle ABC$中,$AB = AC,\angle BAC = 45^{\circ}$.小聪同学利用直尺和圆规完成了如下操作:①作$\angle BAC$的平分线$AM$交$BC$于点$D$;②作边$AB$的垂直平分线$EF$交$AM$于点$P$;③连接$PB,PC$.下列结论错误的是(
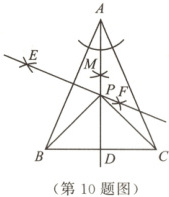
A.$PA = PB = PC$
B.$\angle BPC = 90^{\circ}$
C.$BD = CD$
D.$\angle CPF = 30^{\circ}$
D
)
A.$PA = PB = PC$
B.$\angle BPC = 90^{\circ}$
C.$BD = CD$
D.$\angle CPF = 30^{\circ}$
答案:
10.D
11. 分解因式:$3a - ab =$
a(3-b)
.
答案:
11.a(3-b)
12. 清代诗人袁枚的一首诗《苔》中写道:“白日不到处,青春恰自来.苔花如米小,也学牡丹开.”若苔花的花粉直径是$0.000\ 008\ 4\ m$,则数$0.000\ 008\ 4$用科学记数法表示为
$8.4× 10^{-6}$
.
答案:
$8.4× 10^{-6}$
13. 若$x^2 + mx + 9$是一个完全平方式,则$m$的值是
$\pm 6$
.
答案:
13.$\pm 6$
14. 新情境 生活运用 如图1是一个地铁站入口的双翼闸机,它的双翼展开时,双翼边缘的端点$A$与$B$之间的距离是12 cm,如图2,双翼的边缘$AC = BD = 64\ cm$,且与闸机的侧立面夹角$\angle PCA = \angle QDB = 30^{\circ}$.当双翼收起时,可以通过闸机的物体的最大宽度是


76
cm.

答案:
14.76
15. 如图,点$P$是$\angle AOB$内一定点,点$M,N$分别是射线$OA,OB$上的点,连接$PM,PN,MN$.若当$\triangle PMN$的周长最小时,$\angle MPN = 100^{\circ}$,则$\angle AOB$的度数是
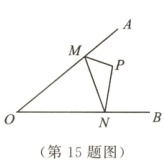
$40^{\circ}$
.
答案:
15.$40^{\circ}$
16. (10分)(1)计算:$(\frac{x}{x - 1} - \frac{1}{x^2 - x}) ÷ \frac{x^2 + 2x + 1}{x^2}$.
(2)解方程:$\frac{x}{x + 1} - 1 = \frac{3}{x - 1}$.
(2)解方程:$\frac{x}{x + 1} - 1 = \frac{3}{x - 1}$.
答案:
16.
(1)$\frac{x}{x + 1}$.
(2)解:方程两边乘$(x + 1)(x - 1)$,
得$x(x - 1) - (x + 1)(x - 1) = 3(x + 1)$.解得$x = -\frac{1}{2}$.
检验:当$x = -\frac{1}{2}$时,$(x + 1)(x - 1) \neq 0$.
$\therefore$原分式方程的解是$x = -\frac{1}{2}$.
(1)$\frac{x}{x + 1}$.
(2)解:方程两边乘$(x + 1)(x - 1)$,
得$x(x - 1) - (x + 1)(x - 1) = 3(x + 1)$.解得$x = -\frac{1}{2}$.
检验:当$x = -\frac{1}{2}$时,$(x + 1)(x - 1) \neq 0$.
$\therefore$原分式方程的解是$x = -\frac{1}{2}$.
查看更多完整答案,请扫码查看


