《2025年点石成金金牌夺冠八年级数学上册人教版辽宁专版》

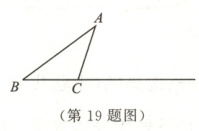
19. (8分)如图,在$\triangle ABC$中,$\angle ACB ＞ 90^{\circ}$,且$AC = BC$.
(1)尺规作图:在$BC$的延长线上作点$D$,使$\angle CAD = 2\angle B$.(保留作图痕迹,不写作法)
(2)连接$AD$,在(1)的条件下,若$AB = AD$,求$\angle B$的度数.

答案：
19.
(1)如图，点D即为所求.
(2)解：$\because AC = BC,\therefore \angle CAB = \angle B$.
$\because AB = AD,\therefore \angle B = \angle ADB$.
由
(1)得，$\angle CAD = 2\angle B$.
$\therefore \angle BAD = \angle CAB + \angle CAD = 3\angle B$.
在$\triangle ABD$中，$\because \angle B + \angle BAD + \angle ADB = 180^{\circ}$，
$\therefore \angle B + 3\angle B + \angle B = 180^{\circ}.\therefore \angle B = 36^{\circ}$.