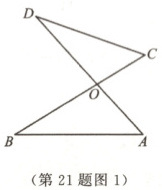
21. (13分)如图1,AD,BC交于点O,连接AB,CD,可以得出两个三角形中的角存在以下数量关系:
①∠DOC = ∠AOB;②∠D + ∠C = ∠A + ∠B.
【提出问题】
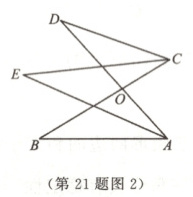
如图2,分别作∠BAD和∠BCD的平分线,两条角平分线相交于点E.求∠E,∠D和∠B之间的数量关系.
【解决问题】
为了解决上述问题,我们先从几个特殊情况开始探究.
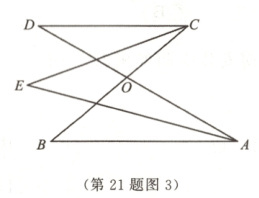
(1)如图3,若AB//CD,∠D = 30°,∠B = 40°,则∠E = _______.
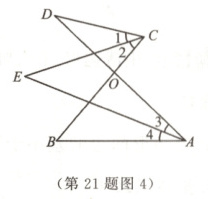
(2)如图4,若AB与CD不平行,∠D = 30°,∠B = 50°,求∠E的度数.
小明是这样思考的,请你帮他完成推理过程:
易证∠D + ∠1 = ∠E + ∠3,∠B + ∠4 = ∠E + ∠2,
∴∠D + ∠1 + ∠B + ∠4 = _______.
∵CE,AE分别是∠BCD和∠BAD的平分线,
∴∠1 = ∠2,∠3 = ∠4.
∴2∠E = _______.
∵∠D = 30°,∠B = 50°,
∴∠E = _______.
(3)在总结前两问结论的基础上,借助图2,请直接写出∠E,∠D和∠B之间的数量关系是_______.
【类比应用】
(4)如图5,∠BAD的平分线AE和∠BCD的平分线CE相交于点E.已知∠D = m°,∠B = n°(m < n),求∠E的度数.

①∠DOC = ∠AOB;②∠D + ∠C = ∠A + ∠B.
【提出问题】
如图2,分别作∠BAD和∠BCD的平分线,两条角平分线相交于点E.求∠E,∠D和∠B之间的数量关系.
【解决问题】
为了解决上述问题,我们先从几个特殊情况开始探究.
(1)如图3,若AB//CD,∠D = 30°,∠B = 40°,则∠E = _______.
(2)如图4,若AB与CD不平行,∠D = 30°,∠B = 50°,求∠E的度数.
小明是这样思考的,请你帮他完成推理过程:
易证∠D + ∠1 = ∠E + ∠3,∠B + ∠4 = ∠E + ∠2,
∴∠D + ∠1 + ∠B + ∠4 = _______.
∵CE,AE分别是∠BCD和∠BAD的平分线,
∴∠1 = ∠2,∠3 = ∠4.
∴2∠E = _______.
∵∠D = 30°,∠B = 50°,
∴∠E = _______.
(3)在总结前两问结论的基础上,借助图2,请直接写出∠E,∠D和∠B之间的数量关系是_______.




【类比应用】
(4)如图5,∠BAD的平分线AE和∠BCD的平分线CE相交于点E.已知∠D = m°,∠B = n°(m < n),求∠E的度数.

答案:
21.
(1)35°
(2)2∠E+∠2+∠3 = ∠D+∠B 40°
(3)2∠E=∠D+∠B
(4)解:如图,延长BC交AD于点F.
∵∠BFD和∠BCD分别是△ABF和△CDF的外角,
∴∠BFD=∠B+∠BAD,∠BCD=∠BFD+∠D.
∴∠BCD=∠B+∠D+∠BAD.
∵AE,CE分别平分∠BAD和∠BCD,
∴∠EAB=$\frac{1}{2}$∠BAD,∠ECB=$\frac{1}{2}$∠BCD.
∵∠E+∠ECB=∠B+∠EAB,
∴∠E=∠B+∠EAB−∠ECB=∠B+$\frac{1}{2}$∠BAD−$\frac{1}{2}$∠BCD=∠B+$\frac{1}{2}$∠BAD−$\frac{1}{2}$(∠B+∠D+∠BAD)=$\frac{1}{2}$(∠B−∠D).
∵∠D=m°,∠B=n°,
∴∠E=$\frac{1}{2}$(n−m)°.
(1)35°
(2)2∠E+∠2+∠3 = ∠D+∠B 40°
(3)2∠E=∠D+∠B
(4)解:如图,延长BC交AD于点F.
∵∠BFD和∠BCD分别是△ABF和△CDF的外角,
∴∠BFD=∠B+∠BAD,∠BCD=∠BFD+∠D.
∴∠BCD=∠B+∠D+∠BAD.
∵AE,CE分别平分∠BAD和∠BCD,
∴∠EAB=$\frac{1}{2}$∠BAD,∠ECB=$\frac{1}{2}$∠BCD.
∵∠E+∠ECB=∠B+∠EAB,
∴∠E=∠B+∠EAB−∠ECB=∠B+$\frac{1}{2}$∠BAD−$\frac{1}{2}$∠BCD=∠B+$\frac{1}{2}$∠BAD−$\frac{1}{2}$(∠B+∠D+∠BAD)=$\frac{1}{2}$(∠B−∠D).
∵∠D=m°,∠B=n°,
∴∠E=$\frac{1}{2}$(n−m)°.
查看更多完整答案,请扫码查看


