《2025年点石成金金牌夺冠八年级数学上册人教版辽宁专版》

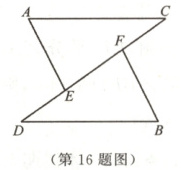
16. (10分)如图,$\angle A = \angle B$,$AC // BD$,点$E$,$F$在$CD$上,且$CF = DE$.求证:$AE = BF$.

答案： 16.证明:
∵AC//BD,
∴∠C=∠D.
∵CF=DE,
∴CF+EF=DE+EF,即CE=DF.
在△AEC和△BFD中，$\begin{cases}∠A=∠B,\\∠C=∠D,\\CE=DF,\end{cases}$
∴△AEC≌△BFD(AAS).
∴AE=BF.

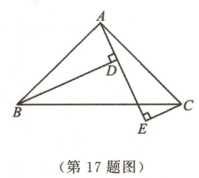
17. (10分)如图,$AB = AC$,$\angle BAC = 90°$,$BD \perp AE$于点$D$,$CE \perp AE$于点$E$.求证:$BD = EC + ED$.

答案： 17.证明:
∵CE⊥AE，BD⊥AE，
∴∠E=∠BDA=90°.
∴∠ABD+∠BAD=90°.
∵∠BAC=∠BAD+∠CAE=90°，
∴∠ABD=∠CAE.
在△ABD和△CAE中，$\begin{cases}∠ABD=∠CAE,\\∠BDA=∠E,\\AB=CA,\end{cases}$
∴△ABD≌△CAE(AAS).
∴BD=AE，DA=EC.
∵AE=DA+ED，
∴BD=EC+ED.

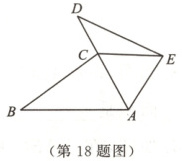
18. (10分)如图,点$C$在线段$AD$上,$AB = AD$,$\angle B = \angle D$,$BC = DE$.
(1)求证:$\triangle ABC \cong \triangle ADE$.
(2)若$\angle BAC = 60°$,$\angle B = 35°$,求$\angle DEA$的度数.

答案： 18.
(1)证明:在△ABC和△ADE中，$\begin{cases}∠B=∠D,\\BC=DE,\\\end{cases}$
∴△ABC≌△ADE(SAS).
(2)由
(1)得,△ABC≌△ADE.
∴∠DAE=∠BAC=60°,∠D=∠B=35°.
∴∠DEA=180°-∠DAE-∠D=85°.