搜索
10. 如图，在△ABC中，∠ABC = 45°，CD⊥AB于点D，BE平分∠ABC，BE⊥AC于点E，交CD于点F，点H是BC的中点，连接DH，交BE于点G. 下列结论：①∠A = 67.5°；②AE = $\frac{1}{2}$BF；③△DGF是等腰三角形；④S四边形ADGE = S四边形GHCE. 其中正确的有（
A.①②③
B.①②④
C.③④
D.①②③④
A
）A.①②③
B.①②④
C.③④
D.①②③④
答案：
10.A
11. 如图，已知△ABC≌△DEF. 若AD = 2，则CF的长是
2
.
答案：
11.2
12. 如图，在△ABC中，AD平分∠BAC，DE⊥AB. 若AC = 2，DE = 1，则△ACD的面积是
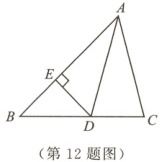
1
.
答案：
12.1
13. 如图，在△ABC中，AD是边BC上的中线，延长AD至点E，使ED = AD，连接BE，EC，则在四边形ABEC中一共有
4
对全等的三角形.
答案：
13.4
14. 如图，在平面直角坐标系中，根据尺规作图的痕迹在第二象限内作出点P(m - 1,2n)，则m与n的数量关系是
$m + 2n = 1$
.
答案：
14.$m + 2n = 1$
15. 如图，AB⊥BC，AD⊥DC，∠BAD = 130°，点M，N分别在BC，CD上. 当△AMN的周长最小时，∠MAN的度数是
$80^{\circ}$
.
答案：
15.$80^{\circ}$ [解析]如图，作点A关于BC和CD的对称点$A_1$，$A_2$，连接$A_1A_2$，交BC于点M，交CD于点N.
$\because A_1M = AM$，$A_2N = AN$，
$\therefore A_1A_2$的长即为$\triangle AMN$周长的最小值.
$\because \angle BAD = 130^{\circ}$，$\therefore \angle A_1 + \angle A_2 = 50^{\circ}$.
$\because \angle BAM = \angle A_1$，$\angle DAN = \angle A_2$，
$\therefore \angle BAM + \angle DAN = 50^{\circ}$.
$\therefore \angle MAN = \angle BAD - (\angle BAM + \angle DAN) = 80^{\circ}$.
15.$80^{\circ}$ [解析]如图，作点A关于BC和CD的对称点$A_1$，$A_2$，连接$A_1A_2$，交BC于点M，交CD于点N.
$\because A_1M = AM$，$A_2N = AN$，
$\therefore A_1A_2$的长即为$\triangle AMN$周长的最小值.
$\because \angle BAD = 130^{\circ}$，$\therefore \angle A_1 + \angle A_2 = 50^{\circ}$.
$\because \angle BAM = \angle A_1$，$\angle DAN = \angle A_2$，
$\therefore \angle BAM + \angle DAN = 50^{\circ}$.
$\therefore \angle MAN = \angle BAD - (\angle BAM + \angle DAN) = 80^{\circ}$.16. (8分)如图，在Rt△ABC中，∠B = 90°，CD//AB，DE⊥AC于点E，且CE = AB. 求证：DC = CA.
答案：
16.证明：$\because DE \perp AC$，$\therefore \angle DEC = \angle B = 90^{\circ}$.
$\because CD // AB$，$\therefore \angle DCB = 180^{\circ} - \angle B = 90^{\circ}$.
$\therefore \angle ACB + \angle DCE = 90^{\circ}$.
$\because \angle ACB + \angle A = 90^{\circ}$，$\therefore \angle DCE = \angle A$.
在$\triangle DCE$和$\triangle CAB$中，$\begin{cases} \angle DCE = \angle A, \\ CE = AB, \\ \angle DEC = \angle B, \end{cases}$
$\therefore \triangle DCE \cong \triangle CAB (ASA)$.$\therefore DC = CA$.
$\because CD // AB$，$\therefore \angle DCB = 180^{\circ} - \angle B = 90^{\circ}$.
$\therefore \angle ACB + \angle DCE = 90^{\circ}$.
$\because \angle ACB + \angle A = 90^{\circ}$，$\therefore \angle DCE = \angle A$.
在$\triangle DCE$和$\triangle CAB$中，$\begin{cases} \angle DCE = \angle A, \\ CE = AB, \\ \angle DEC = \angle B, \end{cases}$
$\therefore \triangle DCE \cong \triangle CAB (ASA)$.$\therefore DC = CA$.
查看更多完整答案，请扫码查看
