《2025年优质课堂导学案七年级数学上册人教版》

1. 几个单项式的和 叫作多项式. 其中，每个单项式叫作多项式的 项，不含字母的项叫作 常数项.

答案： 1.几个单项式的和 项 常数项

2. 多项式里 次数最高项的次数 叫作这个多项式的次数.

答案： 2.次数最高项的次数

3. 单项式与多项式 统称整式.

答案： 3.单项式与多项式

4. 下列式子是多项式的是 (A)

A.$x^{2}+y$
B.$x^{2}y$
C.$-2\pi x^{3}y$
D.$3xy$

答案： 4.A

5. 多项式 $2x^{4}-x^{3}y^{2}+7$ 是 (B)

A.四次三项式
B.五次三项式
C.三次四项式
D.三次五项式

答案： 5.B

6. (2024·武昌期中)对于多项式 $x^{2}y - 3xy - 4$，下列说法正确的是 (C)

A.二次项系数是 3
B.常数项是 4
C.次数是 3
D.项数是 2

答案： 6.C

7. 多项式 $1 + 2xy - 3xy^{2}$ 的次数及最高次项的系数分别是 (A)

A.$3$，$-3$
B.$2$，$-3$
C.$5$，$-3$
D.$3$，$3$

答案： 7.A

8. 多项式 $\frac{1}{2}x + 3x^{2} - 5$ 的各项为 $\frac {1}{2}x$,$3x^{2}$,$-5$，次数最高的项是 $3x^{2}$，一次项系数是 $\frac {1}{2}$，常数项是 $-5$，这个多项式是 二 次 三 项式.

答案： 8.$\frac {1}{2}x$,$3x^{2}$,$-5$ $3x^{2}$,$\frac {1}{2}$,$-5$ 二 三

9. 下列式子：① $-\frac{2}{5}x^{2}$；② $\frac{1}{2}a + bc$；③ $3xy$；④ $0$；⑤ $\frac{3a}{x} + 1$；⑥ $-5a^{2} + a$. 其中单项式有 ①③④，多项式有 ②⑥，整式有 ①②③④⑥(填序号).

答案： 9.①③④ ②⑥ ①②③④⑥

10. 在代数式：$x^{2} + 5$，$-1$，$x^{2} - 3x + 2$，$\pi$，$\frac{5}{x}$，$x^{2} + \frac{1}{x + 1}$ 中，整式有 (B)

A.$3$ 个
B.$4$ 个
C.$5$ 个
D.$6$ 个

答案： 10.B

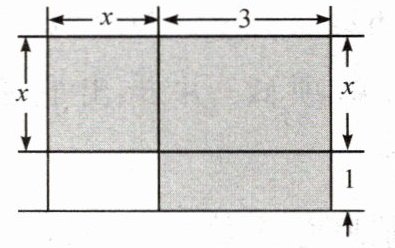
11. 如下图所示：（单位：m）
（1）用含 $x$ 的式子表示阴影部分的面积；
（2）指出所列代数式的次数与项数；
（3）当 $x = 2$ 时，求阴影部分的面积.

答案： 11.解：
(1)$(x^{2}+3x+3)m^{2}$;
(2)所列代数式次数是2,项数是3;
(3)当$x=2$时,原式$=x^{2}+3x+3=2^{2}+3×2+3=13(m^{2})$.

12. 下列说法中，错误的是 (D)

A.$a^{2} - 2ab + b^{2}$ 是二次三项式
B.$x - 5xy^{3} - 1 + 3xy$ 是四次四项式
C.$2x - 3$ 是一次二项式
D.$3x^{2} + xy - 8$ 是四次三项式

答案： 12.D

13. (2024·吉林期末)若多项式 $\frac{1}{2}x^{|m|} + (m - 5)x^{2} + 3$ 是关于 $x$ 的五次三项式，则 $m$ 的值为 $-5$.

答案： 13.$-5$