2. (2024·长寿期中)某工厂生产了一种 T 型零件,该零件由两个长方形组成,其尺寸如图所示. T 型零件的周长为
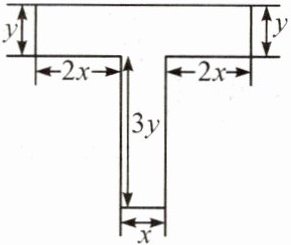
10x+8y
;面积为8xy
,当 $ x = 3 $,$ y = 6 $ 时,面积为144
.
答案:
2.10x+8y 8xy 144
3. 正方体的棱长为 $ a $,体积为 $ V $,则体积 $ V $ 与棱长的关系为
V = a^3
,当 $ a = 3 $ 时,$ V = $27
.
答案:
$3.V = a^3 27$
4. 圆锥的底面半径为 $ r $,高为 $ h $,用代数式表示圆锥的体积 $ V = $
\frac{1}{3}\pi r^{2}h
;当 $ r = 3 dm $,$ h = 8 dm $ 时,$ V = $24\pi
$dm^3$.
答案:
$4.\frac{1}{3}\pi r^{2}h 24\pi$
5. 如图,学校准备修建一个长为 $ a m $,宽为 $ b m $ 的长方形休闲区. 在左右两边修建半径为 $ b m $ 的扇形小广场,图中阴影部分种植花卉.
(1) 用含有 $ a $,$ b $ 的式子表示种植花卉部分的面积:
(2) 当 $ a = 25 $,$ b = 7.5 $ 时,求种植花卉部分的面积($ \pi $ 取 3.14,结果精确到百分位).

(1) 用含有 $ a $,$ b $ 的式子表示种植花卉部分的面积:
(ab - \frac{1}{2}\pi b^{2})m^{2}
;(2) 当 $ a = 25 $,$ b = 7.5 $ 时,求种植花卉部分的面积($ \pi $ 取 3.14,结果精确到百分位).

答案:
$5.(1)(ab - \frac{1}{2}\pi b^{2})m^{2} (2)$解:当a = 25,b = 7.5时,种植花卉部分的面积为$ab - \frac{1}{2}\pi b^{2}=25×7.5 - \frac{1}{2}×3.14×7.5^{2}=187.5 - 88.3125 = 99.1875≈99.19(m^{2})。$所以种植花卉部分的面积为$99.19m^{2}。$
6. 如图,将厚度为 $ h cm $ 的卷筒纸,在半径为 $ r cm $ 的圆筒上卷成半径为 $ R cm $ 的圆筒.
(1) 求出阴影部分圆环的面积 $ S $(用含 $ r $,$ R $ 的式子表示);
(2) 设卷筒纸的总长度为 $ L cm $,则 $ L = \frac{\pi R^2 - \pi r^2}{h} $. 若 $ r = 4 $,$ R = 10 $,$ h = 0.02 $,求这卷卷筒纸的总长度.(其中 $ \pi $ 取 3.14,计算结果精确到米)
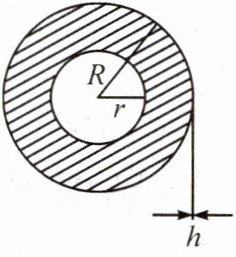
(1) 求出阴影部分圆环的面积 $ S $(用含 $ r $,$ R $ 的式子表示);
(2) 设卷筒纸的总长度为 $ L cm $,则 $ L = \frac{\pi R^2 - \pi r^2}{h} $. 若 $ r = 4 $,$ R = 10 $,$ h = 0.02 $,求这卷卷筒纸的总长度.(其中 $ \pi $ 取 3.14,计算结果精确到米)

答案:
6.解:
(1)阴影部分圆环的面积$S = (\pi R^{2}-\pi r^{2})cm^{2};$
(2)当r = 4,R = 10,h = 0.02时,$L = \frac{\pi R^{2}-\pi r^{2}}{h}=\frac{3.14×10^{2}-3.14×4^{2}}{0.02}=\frac{263.76}{0.02}=13188.13188cm = 131.88m≈132m。$所以这卷卷筒纸的总长度约为132m。
(1)阴影部分圆环的面积$S = (\pi R^{2}-\pi r^{2})cm^{2};$
(2)当r = 4,R = 10,h = 0.02时,$L = \frac{\pi R^{2}-\pi r^{2}}{h}=\frac{3.14×10^{2}-3.14×4^{2}}{0.02}=\frac{263.76}{0.02}=13188.13188cm = 131.88m≈132m。$所以这卷卷筒纸的总长度约为132m。
7. 如图,在一个底为 $ a $,高为 $ h $ 的三角形铁皮上剪去一个半径为 $ r $ 的半圆.
(1) 用含 $ a $,$ h $,$ r $ 的代数式表示剩下铁皮(阴影部分)的面积 $ S $;
(2) 请求出当 $ a = 10 $,$ h = 8 $,$ r = 2 $ 时,$ S $ 的取值($ \pi $ 取 3.14).
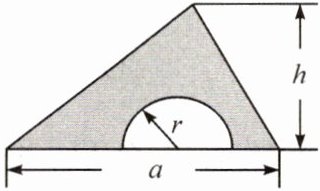
(1) 用含 $ a $,$ h $,$ r $ 的代数式表示剩下铁皮(阴影部分)的面积 $ S $;
(2) 请求出当 $ a = 10 $,$ h = 8 $,$ r = 2 $ 时,$ S $ 的取值($ \pi $ 取 3.14).

答案:
7.解:
(1)由题意可得,$S = S_{三角形}-S_{半圆}=\frac{1}{2}ah - \frac{1}{2}\pi r^{2};$
(2)当a = 10,h = 8,r = 2时,$S=\frac{1}{2}ah - \frac{1}{2}\pi r^{2}=\frac{1}{2}×10×8 - \frac{1}{2}\pi×2^{2}=40 - 2\pi = 33.72。$
(1)由题意可得,$S = S_{三角形}-S_{半圆}=\frac{1}{2}ah - \frac{1}{2}\pi r^{2};$
(2)当a = 10,h = 8,r = 2时,$S=\frac{1}{2}ah - \frac{1}{2}\pi r^{2}=\frac{1}{2}×10×8 - \frac{1}{2}\pi×2^{2}=40 - 2\pi = 33.72。$
查看更多完整答案,请扫码查看


