1. 在解决一些数学问题和实际问题时,把问题中的____用含有____的式子表示出来,就是列代数式。
答案:
1.数量关系 数字、字母和运算符号
3. 用代数式表示“$a$的 2 倍与 3 的差”,正确的是(
A.$2a + 3$
B.$2a - 3$
C.$2(a - 3)$
D.$3 - 2a$
B
)A.$2a + 3$
B.$2a - 3$
C.$2(a - 3)$
D.$3 - 2a$
答案:
3.B
4. 用代数式表示“$a$的 2 倍与 $b$ 的平方的和”,正确的是(
A.$(2a + b)^2$
B.$2(a + b)^2$
C.$2a + b^2$
D.$(a + 2b)^2$
C
)A.$(2a + b)^2$
B.$2(a + b)^2$
C.$2a + b^2$
D.$(a + 2b)^2$
答案:
4.C
5. 2025 长春马拉松于 5 月 25 日在长春体育中心鸣枪开跑,某同学参加了 $7.5$km 健康跑项目,他从起点开始以平均每分钟 $x$km 的速度跑了 $10$min,此时他离健康跑终点的路程为
7.5-10x
km.(用含 $x$ 的代数式表示)
答案:
5.7.5-10x
6. 甲、乙两件衣服单价为 $x$ 元、$y$ 元,在换季时,甲衣服按 4 折,乙衣服按 6 折,这时买这两件衣服各一件,共需
(0.4x+0.6y)
元。
答案:
6.(0.4x+0.6y)
7. 某品牌奶糖 $a$ 元/kg,水果糖 $b$ 元/kg,如果买奶糖 $m$kg,水果糖 $n$kg,那么混合后的糖果每千克
\frac{ma+nb}{m+n}
元。
答案:
$7.\frac{ma+nb}{m+n}$
8. 一项工程,甲单独做需要 $m$ 天,乙单独做需要 $n$ 天。
(1)如果甲单独做了 3 天,完成的工作量是多少?
(2)如果甲单独先做了 2 天,然后乙单独又做了 5 天,甲、乙一共完成的工作量是多少?
(3)如果甲、乙合做了 2 天,乙又单独做了 3 天,甲、乙一共完成的工作量是多少?
(1)如果甲单独做了 3 天,完成的工作量是多少?
(2)如果甲单独先做了 2 天,然后乙单独又做了 5 天,甲、乙一共完成的工作量是多少?
(3)如果甲、乙合做了 2 天,乙又单独做了 3 天,甲、乙一共完成的工作量是多少?
答案:
8.解:
(1)甲完成的工作量是$\frac{3}{m};$
(2)甲、乙一共完成的工作量是$\frac{2}{m}+\frac{5}{n};$
(3)甲、乙一共完成的工作量是$\frac{2}{m}+\frac{5}{n}$
(1)甲完成的工作量是$\frac{3}{m};$
(2)甲、乙一共完成的工作量是$\frac{2}{m}+\frac{5}{n};$
(3)甲、乙一共完成的工作量是$\frac{2}{m}+\frac{5}{n}$
9. 如图是由直角边分别为 $a$,$b$ 的直角三角形和直径为 $b$ 的半圆所构成的图形,求这个图形的面积 $S$。(用含 $a$,$b$,$\pi$ 的代数式表示)
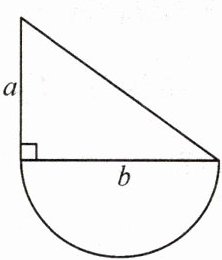

答案:
9.解$:S=\frac{1}{2}ab+(\frac{b}{2})^2\pi×\frac{1}{2}=\frac{1}{2}ab+\frac{1}{8}\pi b^2。$
10. 一辆汽车以 $v_1$km/h 的速度行驶,从 A 城到 B 城需要 $t$(单位:h),如果该车的行驶速度增加 $v_2$km/h,则从 A 城到 B 城需要多少时间?
答案:
10.解:由题意可得,A城到B城的距离为$v_1t$km,该车增加后的速度为(v_1+v_2)km/h,所以从A城到B城需要的时间为\frac{v_1t}{v_1+v_2}(h)。
查看更多完整答案,请扫码查看


