1. 函数 $ y = 2x^{2}-5x - 3 $ 与 $ x $ 轴的交点坐标为
$(-\frac{1}{2},0)$,$(3,0)$
.
答案:
$(-\frac{1}{2},0)$,$(3,0)$
2. 二次函数的图象与 $ x $ 轴的交点坐标为 $ (-3,0) $,$ (1,0) $,且经过点 $ (0,6) $,则该二次函数的表达式为
$y = -2x^2 -4x + 6$
.
答案:
$y = -2x^2 -4x + 6$(或填写$y = -2(x + 1)^2 + 8$ 等其他等价形式,根据具体答案格式要求)
3. 若抛物线 $ y = x^{2}+(m - 2)x - 2m $ 的顶点在 $ x $ 轴上,则 $ m $ 的值是
-2
.
答案:
-2
4. 如图,已知二次函数 $ y_{1}= ax^{2}+bx + c(a\neq0) $ 与一次函数 $ y_{2}= kx + m(k\neq0) $ 的图象交于点 $ A(-2,4) $,$ B(8,2) $,则能使 $ y_{1}>y_{2} $ 成立的 $ x $ 的取值范围是
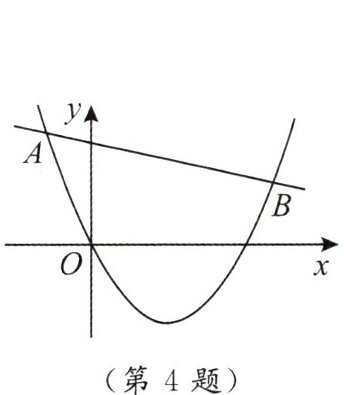
$x<-2$ 或 $x>8$
.
答案:
$x<-2$ 或 $x>8$(或写成区间形式$(-\infty,-2)\cup(8,+\infty)$ ,按题目要求这里填不等式形式)
5. 二次函数 $ y = ax^{2}+bx + c(a\neq0) $ 的图象如图所示,那么下列结论正确的是(
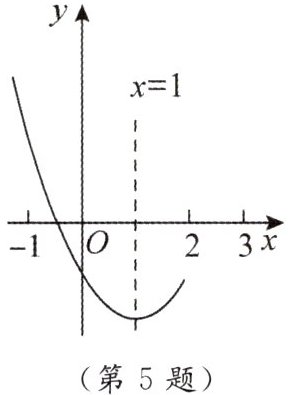
A.$ ac<0 $
B.$ b = 2a $
C.$ b^{2}-4ac<0 $
D.一元二次方程 $ ax^{2}+bx + c = 0(a\neq0) $ 的近似解为 $ x_{1}\approx - 0.5 $,$ x_{2}\approx3.2 $
A
)
A.$ ac<0 $
B.$ b = 2a $
C.$ b^{2}-4ac<0 $
D.一元二次方程 $ ax^{2}+bx + c = 0(a\neq0) $ 的近似解为 $ x_{1}\approx - 0.5 $,$ x_{2}\approx3.2 $
答案:
A
6. 根据下表中二次函数 $ y = ax^{2}+bx + c(a\neq0) $ 的自变量 $ x $ 与函数值 $ y $ 的对应值,判断方程 $ ax^{2}+bx + c = 0(a\neq0,a,b,c $ 为常数)的一个解 $ x $ 的范围是(

A.$ 6<x<6.17 $
B.$ 6.17<x<6.18 $
C.$ 6.18<x<6.19 $
D.$ 6.19<x<6.20 $
C
)
A.$ 6<x<6.17 $
B.$ 6.17<x<6.18 $
C.$ 6.18<x<6.19 $
D.$ 6.19<x<6.20 $
答案:
C
查看更多完整答案,请扫码查看


