6. 如图,在半径为$\sqrt {13}的\odot O$中,弦$AB与CD交于点E$,$\angle DEB = 75^{\circ}$,$AB = 6$,$AE = 1$,则$CD$的长是(

A.$2\sqrt {6}$
B.$2\sqrt {10}$
C.$2\sqrt {11}$
D.$4\sqrt {3}$
]
C
)
A.$2\sqrt {6}$
B.$2\sqrt {10}$
C.$2\sqrt {11}$
D.$4\sqrt {3}$
]
答案:
C
7. 如图,在$\odot O$中,$C是弦AB$上的点,$AC = 2$,$CB = 8$. 连结$OC$,过点$C作DC\perp OC$,与$\odot O交于点D$,则$DC$的长为
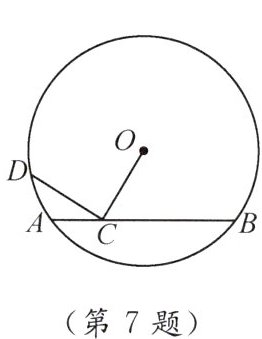
4
.
答案:
4
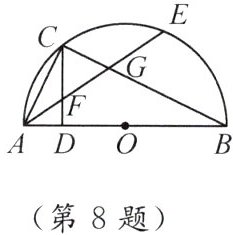
8. 如图,$AB是半圆O$的直径,$AE$为弦,$C为AE$的中点,$CD\perp AB于点D$,交$AE于点F$,$BC交AE于点G$. 求证:$AF = FC$.
]
]

答案:
证明:
1. 连接AC,
∵AB是半圆O的直径,
∴∠ACB=90°(直径所对的圆周角是直角),
∴∠CAB+∠CBA=90°(直角三角形两锐角互余)。
2.
∵CD⊥AB,
∴∠CDA=90°,
∴∠CAB+∠ACD=90°(直角三角形两锐角互余)。
3. 由1、2得∠ACD=∠CBA(同角的余角相等)。
4.
∵C为AE中点,
∴弧AC=弧CE(中点定义),
∴∠CBA=∠CAE(等弧所对的圆周角相等)。
5. 由3、4得∠ACD=∠CAE(等量代换)。
6. 在△AFC中,∠CAE=∠ACD,即∠FAC=∠FCA,
∴AF=FC(等角对等边)。
综上,AF=FC。
1. 连接AC,
∵AB是半圆O的直径,
∴∠ACB=90°(直径所对的圆周角是直角),
∴∠CAB+∠CBA=90°(直角三角形两锐角互余)。
2.
∵CD⊥AB,
∴∠CDA=90°,
∴∠CAB+∠ACD=90°(直角三角形两锐角互余)。
3. 由1、2得∠ACD=∠CBA(同角的余角相等)。
4.
∵C为AE中点,
∴弧AC=弧CE(中点定义),
∴∠CBA=∠CAE(等弧所对的圆周角相等)。
5. 由3、4得∠ACD=∠CAE(等量代换)。
6. 在△AFC中,∠CAE=∠ACD,即∠FAC=∠FCA,
∴AF=FC(等角对等边)。
综上,AF=FC。
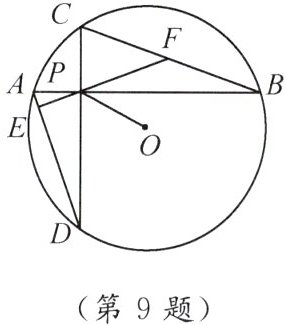
9. 如图,$\odot O的半径为4\sqrt {5}$,$\odot O的两条弦AB\perp CD于点P$,$BC中点为F$,连结$FP并延长交AD于E$.
(1)求证:$EF\perp AD$.
(2)若$AB = 16$,$OP = 6$,求弦$CD$的长.
]
(1)求证:$EF\perp AD$.
(2)若$AB = 16$,$OP = 6$,求弦$CD$的长.
]

答案:
(1)见证明过程;(2)4√15。
查看更多完整答案,请扫码查看


