《2025年全程助学与学习评估九年级数学上册浙教版》

1. 若连结圆上两点的最长线段长为6,则此圆的面积为9π.

答案： $9\pi$

2. $\odot O$的半径为13,圆心$O到直线l的距离d = OD = 5$.在直线$l上有三点P$,$Q$,$R$,且$PD = 12$,$QD = 11$,$RD = 13$,则点$P在\odot O$上,点$Q在\odot O$内,点$R在\odot O$外.

答案： 上，内，外

3. 在$\mathrm{Rt}\triangle ABC$中,$\angle C = 90^{\circ}$,$CD\perp AB$,$AC = 3$,$BC = 4$,若以$C$为圆心,以3为半径作$\odot C$,则点$A在\odot C$上,点$B在\odot C$外,点$D在\odot C$内.

答案： 上，外，内

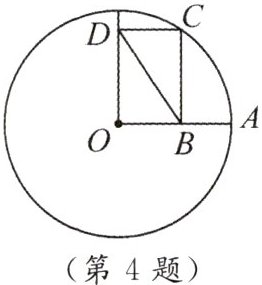
4. 如图,$OA是\odot O$的半径,$B为OA$上一点(且不与点$O$,$A$重合),过点$B作OA的垂线交\odot O于点C$.以$OB$,$BC为边作矩形OBCD$,连结$BD$.若$BD = 10$,$BC = 8$,则$AB$的长为(C)

A.8
B.6
C.4
D.2

答案： C

5. 下列结论正确的是(C)

A.弦是直径
B.长度相等的两条弧一定是等弧
C.半圆是弧
D.过圆心的线段是直径

答案： C

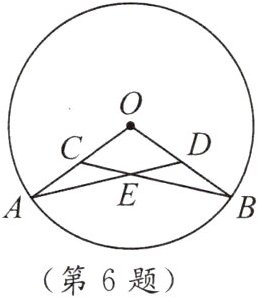
6. 如图,$OA$,$OB为\odot O$的半径,$C$,$D分别为OA$,$OB$的中点.
求证：$\angle A = \angle B$.

答案： 证明：
由题意知$OA$，$OB$为$\odot O$的半径，
所以$OA = OB$。
因为$C$，$D$分别为$OA$，$OB$的中点，
所以$OC=\frac{1}{2}OA$，$OD = \frac{1}{2}OB$，
则$OC = OD$。
在$\triangle OAC$与$\triangle OBD$中，
$\begin{cases}OA = OB\\\angle AOC=\angle BOD\\OC = OD\end{cases}$
根据“边角边”（$SAS$）全等判定定理，可得$\triangle OAC\cong\triangle OBD$。
所以$\angle A=\angle B$。