《2025年全程助学与学习评估九年级数学上册浙教版》

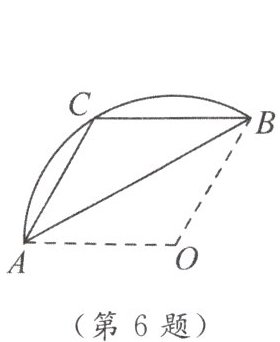
6. 如图，沿弦$AB$折叠扇形纸片$AOB$，圆心$O$恰好落在$\overset{\frown}{AB}$上的点$C$处，若$AB = 4\sqrt{3}$，则四边形$OACB$的面积为8√3.

答案： 8√3

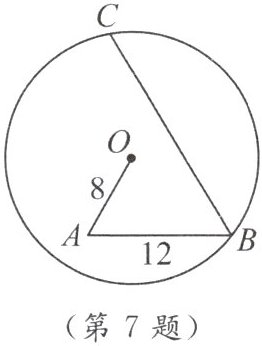
▲7. 如图，在$\odot O$内有折线$OABC$，点$B$在$\odot O$上，其中$OA = 8$，$AB = 12$，$\angle A=\angle B = 60^{\circ}$，则$BC=$16.

答案： 20

▲8. 如图，在$\odot O$中，弦$EF//$弦$CD$（不是直径），直径$AB$分别交$CD$，$EF$于点$M$，$N$，且$A$是$\overset{\frown}{EF}$的中点. 求证：$M$是弦$CD$的中点.

答案： 证明：连接OE，OF，
∵A是$\overset{\frown}{EF}$的中点，
∴$\overset{\frown}{AE}=\overset{\frown}{AF}$，
∴∠AOE=∠AOF，
∵OE=OF，ON=ON，
∴△OEN≌△OFN(SAS)，
∴∠ONE=∠ONF，
∵∠ONE+∠ONF=180°，
∴∠ONE=∠ONF=90°，
∴AB⊥EF，
∵EF//CD，
∴AB⊥CD，
∵AB是直径，
∴M是弦CD的中点.

▲9. 如图，有一座拱桥是圆弧形，它的跨度$AB = 60$米，拱高$PD = 18$米.
（1）求圆弧所在的圆的半径.
（2）当洪水泛滥到跨度只有$30$米时，要采取紧急措施. 若拱顶离水面只有$4$米，即$PE = 4$米时，是否要采取紧急措施？

答案： （1）34米；（2）不需要采取紧急措施。