《2025年全程助学与学习评估九年级数学上册浙教版》

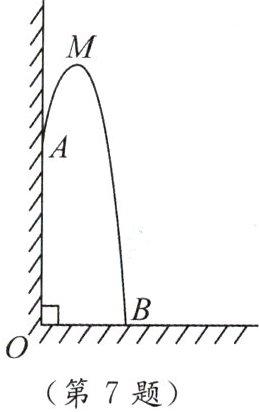
7. 在某幢建筑物内,从 $ 10 $ 米高的窗口 $ A $ 用水管向外喷水,喷出的水流呈抛物线状(抛物线所在平面与墙面垂直,如图). 如果抛物线的最高点 $ M $ 离墙 $ 1 $ 米,离地面 $ \frac { 40 } { 3 } $ 米,则水流落地点 $ B $ 离墙的距离 $ O B $ 是(B)

A.$ 2 $ 米
B.$ 3 $ 米
C.$ 4 $ 米
D.$ 5 $ 米

答案： B

▲8. 某一型号飞机着陆后滑行的距离 $ y ( \mathrm { m } ) $ 与滑行时间 $ x ( \mathrm { s } ) $ 之间的函数表达式是 $ y = 60 x - 1.5 x ^ { 2 } $,该型号飞机着陆后滑行600$ \mathrm { m } $ 才能停下来.

答案： 600

▲9. 某建筑物的窗户如图所示,它的上半部是半圆,下半部是矩形,制造窗框的材料总长(图中所有实线的长度和)为 $ 10 $ 米. 若设窗户上半部的半圆半径为 $ x $ 米,则当 $ x $ 等于多少米时,窗户的透光面积最大？最大面积是多少？

答案： 当$ x = \frac{10}{4 + \pi} $米时，最大面积为$ \frac{50}{4 + \pi} $平方米。

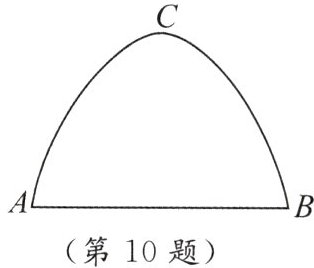
★10. 某单位大门呈抛物线形,如图所示,大门地面宽 $ A B = 4 \mathrm { m } $,顶部 $ C $ 离地面高度为 $ 4.4 \mathrm { m } $. 现有一辆满载货物的汽车欲通过大门,货物顶部距地面 $ 2.8 \mathrm { m } $,装货宽度为 $ 2.4 \mathrm { m } $. 请判断这辆汽车能否顺利通过大门(汽车的宽度小于 $ 2.4 \mathrm { m } $).

答案： 建立平面直角坐标系，设抛物线方程为 $y = ax^{2} + bx + c$（$a \neq 0$），由于大门对称，所以$b=0$，且顶点在y轴，设为$y = ax^{2} + k$。
根据题意，大门地面宽$AB = 4m$，即当$x = \pm 2$时，$y = 0$；
顶部$C$离地面高度为$4.4m$，即当$x = 0$时，$y = 4.4$。
代入得：
$\begin{cases}4a + k = 0, \\k = 4.4.\end{cases}$
解得：
$\begin{cases}a = -1.1, \\k = 4.4.\end{cases}$
所以抛物线方程为：
$y = -1.1x^{2} + 4.4$。
当货物顶部距地面$2.8m$时，即$y = 2.8$，代入方程得：
$2.8 = -1.1x^{2} + 4.4$。
解得：
$x^{2} = \frac{4.4 - 2.8}{1.1} = \frac{1.6}{1.1} = \frac{16}{11}$。
所以，$x = \pm \frac{4}{\sqrt{11}}$。
此时，大门的宽度为两倍的$x$值，即：
$2 × \frac{4}{\sqrt{11}} \approx 2 × 1.2 \approx 2.42(m)$（结果保留两位小数）。
由于$2.42 \gt 2.4$，所以汽车能顺利通过大门。