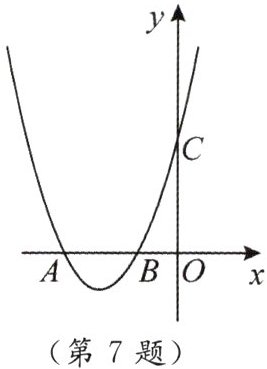
7. 如图,二次函数 $ y_{1}= ax^{2}+bx + 3 $ 的图象与 $ x $ 轴相交于点 $ A(-3,0) $,$ B(-1,0) $,与 $ y $ 轴相交于点 $ C $.
(1)求二次函数的表达式及其图象的顶点坐标.
(2)若一次函数 $ y_{2}= kx + 3 $ 的图象经过二次函数图象的顶点,请根据图象直接写出当 $ y_{1}>y_{2} $ 时 $ x $ 的取值范围.
(1)求二次函数的表达式及其图象的顶点坐标.
(2)若一次函数 $ y_{2}= kx + 3 $ 的图象经过二次函数图象的顶点,请根据图象直接写出当 $ y_{1}>y_{2} $ 时 $ x $ 的取值范围.

答案:
(1)
已知二次函数$y_1 = ax^2 + bx + 3$的图象经过$A(-3,0)$,$B(-1,0)$两点,
将点$A(-3,0)$,$B(-1,0)$代入$y_1 = ax^2 + bx + 3$中,
可得$\begin{cases}9a - 3b + 3 = 0\\a - b + 3 = 0\end{cases}$
由$a - b + 3 = 0$得$b = a + 3$,
将$b = a + 3$代入$9a - 3b + 3 = 0$中,
$9a - 3(a + 3) + 3 = 0$
$9a - 3a - 9 + 3 = 0$
$6a - 6 = 0$
$6a = 6$
解得$a = 1$,
则$b = a + 3 = 1 + 3 = 4$,
所以二次函数的表达式为$y_1 = x^2 + 4x + 3$。
将二次函数$y_1 = x^2 + 4x + 3$化为顶点式:
$y_1 = x^2 + 4x + 3=(x + 2)^2 - 1$
所以其图象的顶点坐标为$(-2,-1)$。
(2)
因为一次函数$y_2 = kx + 3$的图象经过二次函数图象的顶点$(-2,-1)$,
将$(-2,-1)$代入$y_2 = kx + 3$中,
$-2k + 3 = -1$
$-2k = -4$
解得$k = 2$,
所以$y_2 = 2x + 3$。
由$y_1>y_2$,即$x^2 + 4x + 3>2x + 3$,
$x^2 + 4x + 3-(2x + 3)>0$
$x^2 + 2x>0$
$x(x + 2)>0$
则$\begin{cases}x>0\\x + 2>0\end{cases}$或$\begin{cases}x<0\\x + 2<0\end{cases}$
解$\begin{cases}x>0\\x + 2>0\end{cases}$得$x>0$;
解$\begin{cases}x<0\\x + 2<0\end{cases}$得$x< - 2$。
所以当$y_1>y_2$时$x$的取值范围是$x< - 2$或$x>0$。
综上,答案依次为:
(1)$y_1 = x^2 + 4x + 3$,顶点坐标为$(-2,-1)$;
(2)$x< - 2$或$x>0$。
(1)
已知二次函数$y_1 = ax^2 + bx + 3$的图象经过$A(-3,0)$,$B(-1,0)$两点,
将点$A(-3,0)$,$B(-1,0)$代入$y_1 = ax^2 + bx + 3$中,
可得$\begin{cases}9a - 3b + 3 = 0\\a - b + 3 = 0\end{cases}$
由$a - b + 3 = 0$得$b = a + 3$,
将$b = a + 3$代入$9a - 3b + 3 = 0$中,
$9a - 3(a + 3) + 3 = 0$
$9a - 3a - 9 + 3 = 0$
$6a - 6 = 0$
$6a = 6$
解得$a = 1$,
则$b = a + 3 = 1 + 3 = 4$,
所以二次函数的表达式为$y_1 = x^2 + 4x + 3$。
将二次函数$y_1 = x^2 + 4x + 3$化为顶点式:
$y_1 = x^2 + 4x + 3=(x + 2)^2 - 1$
所以其图象的顶点坐标为$(-2,-1)$。
(2)
因为一次函数$y_2 = kx + 3$的图象经过二次函数图象的顶点$(-2,-1)$,
将$(-2,-1)$代入$y_2 = kx + 3$中,
$-2k + 3 = -1$
$-2k = -4$
解得$k = 2$,
所以$y_2 = 2x + 3$。
由$y_1>y_2$,即$x^2 + 4x + 3>2x + 3$,
$x^2 + 4x + 3-(2x + 3)>0$
$x^2 + 2x>0$
$x(x + 2)>0$
则$\begin{cases}x>0\\x + 2>0\end{cases}$或$\begin{cases}x<0\\x + 2<0\end{cases}$
解$\begin{cases}x>0\\x + 2>0\end{cases}$得$x>0$;
解$\begin{cases}x<0\\x + 2<0\end{cases}$得$x< - 2$。
所以当$y_1>y_2$时$x$的取值范围是$x< - 2$或$x>0$。
综上,答案依次为:
(1)$y_1 = x^2 + 4x + 3$,顶点坐标为$(-2,-1)$;
(2)$x< - 2$或$x>0$。
8. 小慈为探索函数 $ y= \sqrt{x^{2}-2x + 4} $ 的性质,通过以下过程画出图象.
(1)列表:请将以下表格中的空白处填写完整;

(2)将表中已知的点描在平面直角坐标系中,并用光滑的曲线画出函数图象;
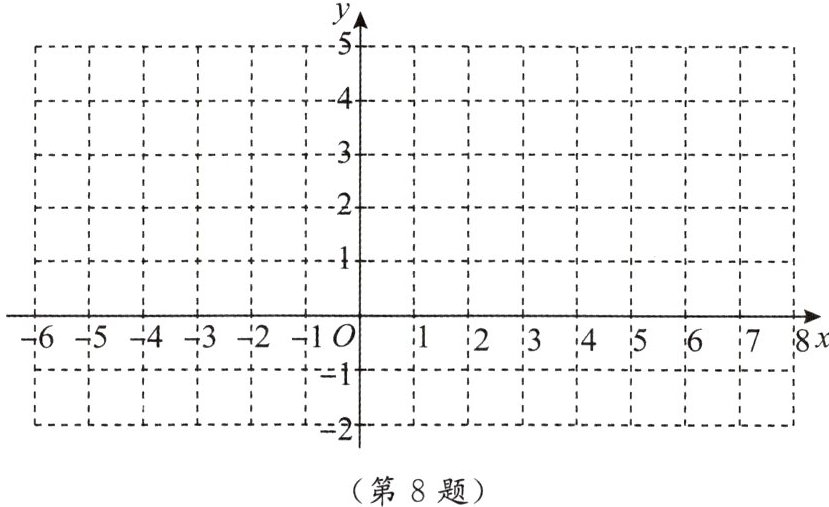
▲(3)从图象可知,图象上纵坐标是横坐标 $ 3 $ 倍的点的横坐标 $ x $ 应符合的条件是(
A. $ 0<x<0.5 $
B. $ 0.5<x<1 $
C. $ 1<x<1.5 $
D. $ 1.5<x<2 $
(1)列表:请将以下表格中的空白处填写完整;

(2)将表中已知的点描在平面直角坐标系中,并用光滑的曲线画出函数图象;

▲(3)从图象可知,图象上纵坐标是横坐标 $ 3 $ 倍的点的横坐标 $ x $ 应符合的条件是(
B
)A. $ 0<x<0.5 $
B. $ 0.5<x<1 $
C. $ 1<x<1.5 $
D. $ 1.5<x<2 $
(1) 2;2
答案:
(1) 2;2
(3) B
(1) 2;2
(3) B
查看更多完整答案,请扫码查看


