▲6. 如图,$AB为\odot O$的一固定直径,它把$\odot O$分成上、下两个半圆,自上半圆上一点$C作弦CD\perp AB$,$\angle OCD的平分线交\odot O于点P$,当点$C$在上半圆(不包括$A$,$B$两点)上移动时,点$P$(
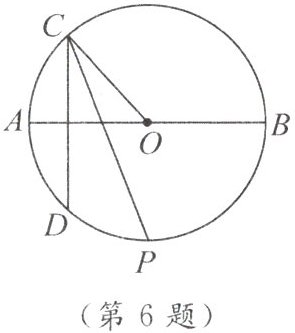
A.到$CD$的距离保持不变
B.位置不变
C.等分$\overset{\frown}{BD}$
D.随$C$点的移动而移动
]
B
)
A.到$CD$的距离保持不变
B.位置不变
C.等分$\overset{\frown}{BD}$
D.随$C$点的移动而移动
]
答案:
B
7. 如图,$\odot O的两条弦AF$,$BE的延长线交于C$点,$\angle ACB的平分线CD过点O$,请直接写出图中一对相等的线段:
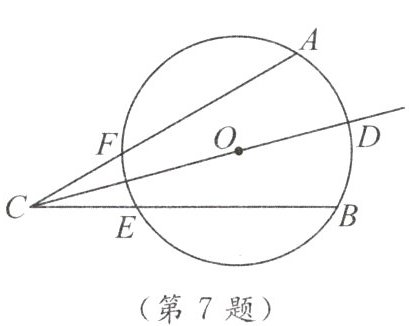
AF=BE
。
答案:
【解析】过点O作OM⊥AC于M,ON⊥BC于N。因为CD平分∠ACB,O在CD上,所以OM=ON(角平分线上的点到角两边距离相等)。OM、ON分别为弦AF、BE的弦心距,同圆中弦心距相等则弦相等,故AF=BE。
【答案】AF=BE
【答案】AF=BE
8. 如图,已知$\odot O的弦AB$,$E$,$F是\overset{\frown}{AB}$上两点,且$\overset{\frown}{AE}= \overset{\frown}{BF}$,$OE$,$OF分别交AB于点C$,$D$。求证:$AC = BD$。
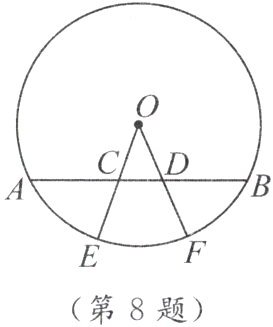

答案:
连接$OA,OB$。
由于$\overset{\frown}{AE} = \overset{\frown}{BF}$,
根据等弧所对的圆心角相等,
所以$\angle AOE = \angle BOF$。
因为$OA = OB$(半径相等),
根据等腰三角形的性质,$\angle OAB = \angle OBA$,
在$\triangle OAC$和$\triangle OBD$中,
$\angle AOC = \angle BOD$(由$\angle AOE = \angle BOF$得出),
$OA = OB$(半径相等),
$\angle OAC = \angle OBD$(等腰三角形的底角相等),
根据角边角全等判定,
所以$\triangle OAC \cong \triangle OBD$,
由于全等三角形的对应边相等,
所以$AC = BD$。
由于$\overset{\frown}{AE} = \overset{\frown}{BF}$,
根据等弧所对的圆心角相等,
所以$\angle AOE = \angle BOF$。
因为$OA = OB$(半径相等),
根据等腰三角形的性质,$\angle OAB = \angle OBA$,
在$\triangle OAC$和$\triangle OBD$中,
$\angle AOC = \angle BOD$(由$\angle AOE = \angle BOF$得出),
$OA = OB$(半径相等),
$\angle OAC = \angle OBD$(等腰三角形的底角相等),
根据角边角全等判定,
所以$\triangle OAC \cong \triangle OBD$,
由于全等三角形的对应边相等,
所以$AC = BD$。
▲9. 如图,$A$,$B$,$C是\odot O$上三点,$\angle AOB = 120^{\circ}$,$C是\overset{\frown}{AB}$的中点,试判断四边形$OACB$形状,并说明理由。
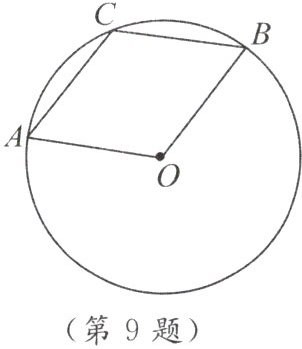

答案:
四边形OACB是菱形。理由如下:
∵A,B,C是⊙O上三点,
∴OA=OB=OC(同圆半径相等)。
∵C是$\overset{\frown}{AB}$的中点,
∴$\overset{\frown}{AC}=\overset{\frown}{BC}$,
∴∠AOC=∠COB(等弧所对圆心角相等)。
∵∠AOB=120°,
∴∠AOC=∠COB=60°。
在△OAC中,OA=OC,∠AOC=60°,
∴△OAC是等边三角形(有一个角为60°的等腰三角形是等边三角形),
∴AC=OA。
同理,△OBC是等边三角形,BC=OB。
∵OA=OB,
∴OA=AC=BC=OB,
∴四边形OACB是菱形(四边相等的四边形是菱形)。
∵A,B,C是⊙O上三点,
∴OA=OB=OC(同圆半径相等)。
∵C是$\overset{\frown}{AB}$的中点,
∴$\overset{\frown}{AC}=\overset{\frown}{BC}$,
∴∠AOC=∠COB(等弧所对圆心角相等)。
∵∠AOB=120°,
∴∠AOC=∠COB=60°。
在△OAC中,OA=OC,∠AOC=60°,
∴△OAC是等边三角形(有一个角为60°的等腰三角形是等边三角形),
∴AC=OA。
同理,△OBC是等边三角形,BC=OB。
∵OA=OB,
∴OA=AC=BC=OB,
∴四边形OACB是菱形(四边相等的四边形是菱形)。
查看更多完整答案,请扫码查看


